
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

【答案】(1)抛物线的解析式为y=![]() x2﹣
x2﹣![]() x﹣1;(2)p=﹣
x﹣1;(2)p=﹣![]() (t﹣2)2+
(t﹣2)2+![]() ,当t=2时,p有最大值
,当t=2时,p有最大值![]() .(3)“落点”的个数有4个,点A1坐标为(
.(3)“落点”的个数有4个,点A1坐标为(![]() ,0)或(
,0)或(![]() ).
).
【解析】
试题分析:(1)把点B的坐标代入直线解析式求出m的值,再把点C的坐标代入直线求解即可得到n的值,然后利用待定系数法求二次函数解析式解答;(2)令y=0求出点A的坐标,从而得到OA、OB的长度,利用勾股定理列式求出AB的长,然后根据两直线平行,内错角相等可得∠ABO=∠DEF,再解直角三角形用DE表示出EF、DF,根据矩形的周长公式表示出p,利用直线和抛物线的解析式表示DE的长,整理即可得到P与t的关系式,再利用二次函数的最值问题解答;(3)根据逆时针旋转角为90°可得A1O1∥y轴时,B1O1∥x轴,旋转角是180°判断出A1O1在x轴上,B1O1∥y轴,根据B1纵坐标为1,求出B1横坐标即可解决问题.
试题解析:(1)∵直线l:y=![]() x+m经过点B(0,﹣1),
x+m经过点B(0,﹣1),
∴m=﹣1,
∴直线l的解析式为y=![]() x﹣1,
x﹣1,
∵直线l:y=![]() x﹣1经过点C(4,n),
x﹣1经过点C(4,n),
∴n=![]() ×4﹣1=2,
×4﹣1=2,
∵抛物线y=![]() x2+bx+c经过点C(4,2)和点B(0,﹣1),
x2+bx+c经过点C(4,2)和点B(0,﹣1),
∴ ,
,
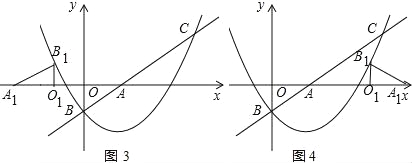
解得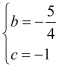 ,
,
∴抛物线的解析式为y=![]() x2﹣
x2﹣![]() x﹣1;
x﹣1;
(2)令y=0,则![]() x﹣1=0,
x﹣1=0,
解得x=![]() ,
,
∴点A的坐标为(![]() ,0),
,0),
∴OA=![]() ,
,
在Rt△OAB中,OB=1,
∴AB=![]() =
=![]() ,
,
∵DE∥y轴,
∴∠ABO=∠DEF,
在矩形DFEG中,EF=DEcos∠DEF=DE![]() =
=![]() DE,
DE,
DF=DEsin∠DEF=DE![]() =
=![]() DE,
DE,
∴p=2(DF+EF)=2(![]() +
+![]() )DE=
)DE=![]() DE,
DE,
∵点D的横坐标为t(0<t<4),
∴D(t,![]() t2﹣
t2﹣![]() t﹣1),E(t,
t﹣1),E(t,![]() t﹣1),
t﹣1),
∴DE=(![]() t﹣1)﹣(
t﹣1)﹣(![]() t2﹣
t2﹣![]() t﹣1)=﹣
t﹣1)=﹣![]() t2+2t,
t2+2t,
∴p=![]() ×(﹣
×(﹣![]() t2+2t)=﹣
t2+2t)=﹣![]() t2+
t2+![]() t,
t,
∵p=﹣![]() (t﹣2)2+
(t﹣2)2+![]() ,且﹣
,且﹣![]() <0,
<0,
∴当t=2时,p有最大值![]() .
.
(3)“落点”的个数有4个,如图1,图2,图3,图4所示.
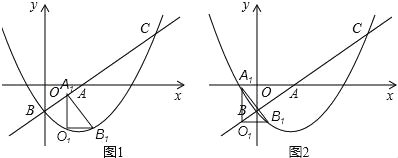
如图3,图4中,B1O1=BO=1,则![]() x2﹣
x2﹣![]() x﹣1=1,解得x=
x﹣1=1,解得x=![]() ,
,
∵A1O1=![]() ,
,
∴图3中,OA1=OO1+A1O1═![]() ,图4中OA1═OO1+O1A1=
,图4中OA1═OO1+O1A1=![]()
∴点A1坐标为(![]() ,0)或(
,0)或(![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
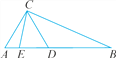
【题目】如图,在△ABC中,AD=AC,BE=BC.
(1)若∠ACB=96°,求∠DCE的度数.
(2)问:∠DCE与∠A,∠B之间存在怎样的数量关系(直接写出答案)?
查看答案和解析>>
科目:初中数学 来源: 题型:
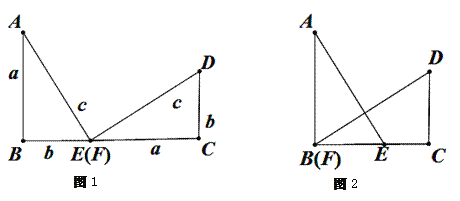
【题目】(1)以a,b为直角边,c为斜边作两个全等的Rt△ABE与Rt△FCD拼成如图1所示的图形,使B,E,F,C四点在一条直线上(此时E,F重合),可知△ABE ≌△FCD,AE![]() DF,请你证明:
DF,请你证明:![]() ;
;
(2)在(1)中,固定△FCD,再将△ABE沿着BC平移到如图2的位置(此时B,F重合),请你重新证明:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五位学生的一分钟跳绳成绩分布为(单位:个):126,134,134,135,160,在统计数据时,把其中一个134写出了124,则计算结果不受影响的是( )
A.中位数B.众数C.方差D.平均数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推广阳光体育“大课间”活动,我市某中学决定在学生中开设A:实心球,B:立定跳远,C:跳绳,D:跑步四种活动项目.为了了解学生对四种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图①②的统计图.请结合图中的信息解答下列问题:
(1)在这项调查中,共调查了多少名学生?
(2)请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比,并将两个统计图补充完整;
(3)若调查到喜欢“跳绳”的5名学生中有3名男生,2名女生.现从这5名学生中任意抽取2名学生.请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据科学家估计,地球的年龄大约是4 550 000 000年,将4 550 000 000用科学记数法表示为( )
A.455×107B.0.455×1010C.45.5×108D.4.55×109
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郑州市雾霾天气趋于严重,丹尼斯商场根据民众健康需要,代理销售每台 进价分别为600元、560元的A、B两种型号的空气净化器,如表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 4台 | 5台 | 7100元 |
第二周 | 6台 | 10台 | 12600元 |
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A,B两种型号的空气净化器的销售单价;
(2)若商场准备用不多于17200元的金额再采购这两种型号的空气净化器共30台,超市销售完这30台空气净化器能否实现利润为6200元的目标,若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
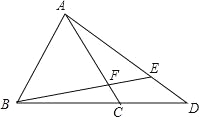
【题目】如图,△ABC是等边三角形,延长BC至D,连接AD,在AD上取一点E,连接BE交AC于F,若AF+CD=AD,DE=2,AF=4,则AD长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《济南市人口发展“十三五“规划》近日出炉,根据规划,到2020年全市常住人口将达到70万人,城区常住人口规模达500万人以上,迈入特大城市行列,770万这个数用科学记数法表示为( )
A. 77×105 B. 7.7×105 C. 7.7×106 D. 0.77×107
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com