
����Ŀ��Ϊ�ƹ�������������μ����������ij��ѧ������ѧ���п���A��ʵ����B��������Զ��C��������D���ܲ����ֻ��Ŀ��Ϊ���˽�ѧ����������Ŀ��ϲ������������ȡ�˲���ѧ�����е��飬�������������Ƴ���ͼ�٢���ͳ��ͼ������ͼ�е���Ϣ����������⣺
��1������������У��������˶�����ѧ����
��2������㱾�������ϲ����������Զ����ѧ����������ռ�ٷֱȣ���������ͳ��ͼ����������
��3�������鵽ϲ������������5��ѧ������3��������2��Ů�����ִ���5��ѧ���������ȡ2��ѧ�������û���״ͼ���б��ķ���������պó鵽ͬ�Ա�ѧ���ĸ��ʣ�

���𰸡���1����������150��ѧ������2�����������ϲ����������Զ����ѧ������Ϊ45�ˣ�����ռ�ٷֱ�0%��ͼ�����������3��![]() ��
��
�������������������1����A������������ռ�İٷֱȣ�������������ѧ��������2���ó�����������ȥA��C��D�����������ϲ����������Զ����ѧ���������ٳ��Ա������ѧ�����������ռ�İٷֱȣ��ٻ�ͼ���ɣ���3����A��ʾ������B��ʾŮ������������ͼ���ٸ��ݸ��ʹ�ʽ���м��㼴�ɣ�
�����������1���������⣬�ã�15��10%=150���ˣ���
������������У���������150��ѧ����
��2�����ε�����ϲ����������Զ����ѧ������Ϊ��150��15��60��30=45���ˣ���
��������Զ����ѧ��ռ������ѧ���ٷֱ�Ϊ�� ![]() ��100%=30%��
��100%=30%��
��ȫͼ�����£�

��3����A��ʾ������B��ʾŮ������ͼ���£�

����20�������ͬ�Ա�ѧ���������8�֣���պó鵽ͬ�Ա�ѧ���ĸ�����![]() =
=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ� ��
A.ͬһƽ���ڲ��ཻ�����߶α�ƽ��
B.ͬһƽ���ڲ��ཻ�������߱�ƽ��
C.ͬһƽ���ڲ��ཻ��һ���߶���һ��ֱ�߱�ƽ��
D.ͬһƽ���ڲ��ཻ������ֱ�߱�ƽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ŀǰ���ܵ��ڸ������ѻ����ռ�������ij�������ؼ���ũ������ƹ㣬Ϊ��Ӧ���٣����������̳�����4200Ԫ�������ͺ��������ֽ��ܵƣ��������ͺŽ��ܵƵĽ��ۡ��ۼ������
���ۣ�Ԫ/ֻ�� | �ۼۣ�Ԫ/ֻ�� | |
���� | 25 | 30 |
���� | 45 | 60 |
�ر�˵����ë����=�ۼ۩�����
��1�����������̳����ۼ��ͽ��ܵ�һֻë����������Ԫ��
��2�����������̳�����ף������ֽ��ܵƹ�100ֻ���������˼��ͽ��ܵƶ���ֻ��
��3�����ڳ��������̳��������ͽ��ܵ�mֻ����������ܵ�ʱ�����ë����ΪyԪ��
�ٵ�y=1080ʱ����m��ֵ��
�ڳ��������̳��ѹ������������ͺŽ��ܵ�ȫ��������ʱ������õ�ë��������� _Ԫ������ֱ��д���𰸣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ֱ��l��y=![]() x+m��x�ᡢy��ֱ��ڵ�A�͵�B��0����1����������y=
x+m��x�ᡢy��ֱ��ڵ�A�͵�B��0����1����������y=![]() x2+bx+c������B����ֱ��l����һ������ΪC��4��n����
x2+bx+c������B����ֱ��l����һ������ΪC��4��n����
��1����n��ֵ�������ߵĽ���ʽ��
��2����D���������ϣ�DE��y�ύֱ��l�ڵ�E����F��ֱ��l�ϣ����ı���DFEGΪ���Σ���ͼ2�������D�ĺ�����Ϊt��0��t��4��������DFEG���ܳ�Ϊp����p��t�ĺ�����ϵʽ�Լ�p�����ֵ��
��3������AOB��ƽ����ij��M��ת90���180�㣬�õ���A1O1B1����A��O��B�Ķ�Ӧ��ֱ��ǵ�A1��O1��B1������A1O1B1����������ǡ�������������ϣ���ô���Ǿͳ������ĵ�Ϊ����㡱����ֱ��д������㡱�ĸ�������ת180��ʱ��A1�ĺ����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A���߶�BC��һ������ABD����ACE���ǵȱ���������
(1)����BE��DC����֤��BE��DC.
(2)��ͼ��������ABD�Ƶ�A˳ʱ����ת�õ���AB��D��.
������ת��Ϊ__ _��ʱ����AD������AE����
�����������������ӳ�DD����CE�ڵ�P������BD����CD��.���߶�AB��AC����ʲô������ϵʱ����BDD������CPD��ȫ�ȣ�������֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����m��2���෴����5����ô��m��ֵ�ǣ�������
A. +7 B. ��7 C. +3 D. ��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������̽���⣺ϸ�Ĺ۲���ͼ�����������ʽ��Ȼ����������
OA22=(![]() )2��1��2
)2��1��2 ![]() ��
��
OA32=(![]() )2��1��3
)2��1��3 ![]() ��
��
OA42=(![]() )2��1��4
)2��1��4 ![]() ��
��
��գ���1����д������n��nΪ���������ĵ�ʽSn=�� ����
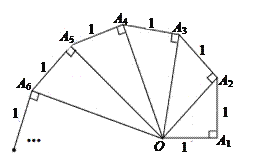
��2�������OA10=�� ����
��3����S12+S22+S32+��+S102��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com