
【题目】如图①,A是线段BC上一点,△ABD和△ACE都是等边三角形.
(1)连结BE,DC,求证:BE=DC.
(2)如图②,将△ABD绕点A顺时针旋转得到△AB′D′.
①当旋转角为__ _度时,边AD′落在AE上.
②在①的条件下,延长DD′交CE于点P,连结BD′,CD′.当线段AB,AC满足什么数量关系时,△BDD′与△CPD′全等?并给予证明.

【答案】(1)证明见解析(2)①60°②当AC=2AB时,△BDD′与△CPD′全等
【解析】试题分析:(1)根据等边三角形的性质可得AB=AD,AE=AC,∠BAD=∠CAE=60°,然后求出∠BAE=∠DAC,再利用“边角边”证明△BAE和△DAC全等,根据全等三角形对应边相等即可得证;(2)①求出∠DAE,即可得到旋转角度数;②当AC=2AB时,△BDD′与△CPD′全等.根据旋转的性质可得AB=BD=DD′=AD′,利用SSS证得△ABD′≌△DBD′,可得∠ABD′=∠DBD′=30°,同理∠AD′B=∠DD′B=30°,所以DP∥BC.再证得∠DBD'=∠PCD',BD'=CD',∠DD'B=∠PD'C,然后利用“角边角”证明△BDD′≌△CPD′即可.
试题解析:
(1)∵△ABD和△ACE都是等边三角形.
∴AB=AD,AE=AC,∠BAD=∠CAE=60°,
∴∠BAD+∠DAE=∠CAE+∠DAE,
即∠BAE=∠DAC.
在△BAE和△DAC中,
∵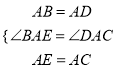
∴△BAE≌△DAC(SAS).∴BE=DC.
(2)①∵∠BAD=∠CAE=60°,
∴∠DAE=180°-60°×2=60°.
∵边AD′落在AE上,
∴旋转角=∠DAE=60°.
②当AC=2AB时,△BDD′与△CPD′全等.
证明如下:
由旋转可知,AB′与AD重合,
∴AB=DB=DD′=AD′.
又∵BD′=BD′,∴△ABD′≌△DBD′(SSS).
∴∠ABD′=∠DBD′=![]() ∠ABD=
∠ABD=![]() ×60°=30°.
×60°=30°.
同理,∠AD′B=∠DD′B=30°,∴DP∥BC.
∵△ACE是等边三角形,
∴AC=AE=CE,∠ACE=60°.
∵AC=2AB,∴AE=2AD′.
∴∠PCD′=∠ACD′=![]() ∠ACE=
∠ACE=![]() ×60°=30°.
×60°=30°.
∴∠ABD′=∠ACD′.∴BD′=CD′.
∵DP∥BC,∴∠PD′C=∠ACD′=30°.
∴∠DBD′=∠DD′B=∠PCD′=∠PD′C=30°.
在△BDD′与△CPD′中,
∵
∴△BDD′≌△CPD′(ASA).


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】实验室里,水平桌面上有甲、乙、丙三个相 同高度的圆柱形容器(容器足够高),底面半径之比为1:2:1,用两个相同的管子在10cm高度处连通(即管子底部离容器底10cm),现三个容器中,只有乙中有水,水位高4cm,如图所示.若每分钟同时向甲和丙注入相同量的水,开始注水1分钟,甲的水位上升3cm.则开始注入 分钟水量后,甲的水位比乙高1cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推广阳光体育“大课间”活动,我市某中学决定在学生中开设A:实心球,B:立定跳远,C:跳绳,D:跑步四种活动项目.为了了解学生对四种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图①②的统计图.请结合图中的信息解答下列问题:
(1)在这项调查中,共调查了多少名学生?
(2)请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比,并将两个统计图补充完整;
(3)若调查到喜欢“跳绳”的5名学生中有3名男生,2名女生.现从这5名学生中任意抽取2名学生.请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郑州市雾霾天气趋于严重,丹尼斯商场根据民众健康需要,代理销售每台 进价分别为600元、560元的A、B两种型号的空气净化器,如表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 4台 | 5台 | 7100元 |
第二周 | 6台 | 10台 | 12600元 |
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A,B两种型号的空气净化器的销售单价;
(2)若商场准备用不多于17200元的金额再采购这两种型号的空气净化器共30台,超市销售完这30台空气净化器能否实现利润为6200元的目标,若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过∠AOB的平分线上一点C作CD∥OB交OA于点D,E是线段OC的中点,过点E作直线分别交射线CD,OB于点M,N,探究线段OD,ON,DM之间的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学张老师在课堂上提出一个问题:“通过探究知道: ![]() ≈1.414…,它是个无限不循环小数,也叫无理数,它的整数部分是1,那么有谁能说出它的小数部分是多少”,小明举手回答:它的小数部分我们无法全部写出来,但可以用
≈1.414…,它是个无限不循环小数,也叫无理数,它的整数部分是1,那么有谁能说出它的小数部分是多少”,小明举手回答:它的小数部分我们无法全部写出来,但可以用 ![]() ﹣1来表示它的小数部分,张老师夸奖小明真聪明,肯定了他的说法.现请你根据小明的说法解答: 已知8+
﹣1来表示它的小数部分,张老师夸奖小明真聪明,肯定了他的说法.现请你根据小明的说法解答: 已知8+ ![]() =x+y,其中x是一个整数,0<y<1,求2x+(y﹣
=x+y,其中x是一个整数,0<y<1,求2x+(y﹣ ![]() )2016的值.
)2016的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),是两个全等的直角三角形(直角边分别为a,b,斜边为c)。
(1)用这样的两个三角形构造成如图(2)的图形,利用这个图形,证明:a2+b2=c2;
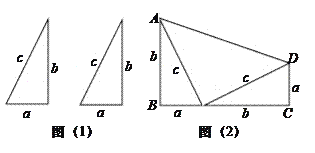
(2)用这样的两个三角形可以拼出多种四边形,画出周长最大的四边形;当a=2,b=4时,求这个四边形的周长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com