
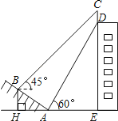
【题目】如图,某大楼的顶部树有一块广告牌CD,小明在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度![]() ,AB=10米,AE=15米.
,AB=10米,AE=15米.
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() )
)
【答案】(1)5;(2)2.7米.
【解析】
试题分析:(1)、根据坡度求出∠BAH的度数,然后求出BH的长度;(2)、根据Rt△BGC和Rt△ADE的三角形函数分别求出CG和DE的长度,然后根据CD=CG+GE-DE进行求解.
试题解析:(1)、 过B作BG⊥DE于G,Rt△ABF中,i=tan∠BAH=
过B作BG⊥DE于G,Rt△ABF中,i=tan∠BAH=![]()
∴∠BAH=30°,∴BH=![]() AB=5;
AB=5;
(2)、由(1)得:BH=5,AH=5![]() ,∴BG=AH+AE=5
,∴BG=AH+AE=5![]() +15,
+15,
Rt△BGC中,∠CBG=45°,∴CG=BG=5![]() +15.
+15.
Rt△ADE中,∠DAE=60°,AE=15,∴DE=![]() AE=15
AE=15![]() .
.
∴CD=CG+GE﹣DE=5![]() +15+5﹣15
+15+5﹣15![]() =20﹣10
=20﹣10![]() ≈2.7m.
≈2.7m.
答:宣传牌CD高约2.7米.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=90°,AB=AC,∠ABC的平分线BD交AC于点D,CE⊥BD,交BD的延长线于点E.试猜想CE与BD的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,O是AB上一点,以OA为半径的⊙O经过点D。

(1)求证:BC是⊙O切线;
(2)若BD=5,DC=3,求AC的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种水果第一天以2元/斤的价格卖出a斤,第二天以1.5元/斤的价格卖出b斤第三天以1.2元/斤的价格卖出c斤,求:
(1)这三天一共卖出水果多少斤?
(2)这三天一共卖得多少钱?
(3)这三天平均售价是多少?并计算当a=30,b=40,c=45时,平均售价是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
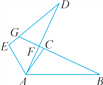
【题目】如图,△ABC≌△ADE,已知点C和点E是对应点,BC的延长线分别交AD,DE于点F,G,且∠DAC=10°,∠B=∠D=25°,∠EAB=120°,试求∠DFB和∠DGB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=40°,分别以AB,AC为边作两个等腰三角形ABD和ACE,且AB=AD,AC=AE,∠BAD=∠CAE=90°.

(1)求∠DBC的度数.
(2)求证:BD=CE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com