
【题目】如图,在△ABC中,AB=AC,∠BAC=40°,分别以AB,AC为边作两个等腰三角形ABD和ACE,且AB=AD,AC=AE,∠BAD=∠CAE=90°.

(1)求∠DBC的度数.
(2)求证:BD=CE.
 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
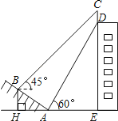
【题目】如图,某大楼的顶部树有一块广告牌CD,小明在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度![]() ,AB=10米,AE=15米.
,AB=10米,AE=15米.
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(a,b)与点B(2,2)是关于原点O的对称点,则( )
A.a=﹣2,b=﹣2
B.a=﹣2,b=2
C.a=2,b=﹣2
D.a=2,b=2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知在△ABC中,∠A=90°,∠B=67.5°,请画一条直线,把这个三角形分割成两个等腰三角形(请你选用下面给出的备用图,把所有不同的分割方法都画出来.只需画图,不必说明理由,但要在图中标出相等两角的度数).
(2)已知在△ABC中,∠C是其最小的内角,过顶点B的一条直线把这个三角形分割成了两个等腰三角形,请探求∠ABC与∠C之间的关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备食建一个面积为200m2的矩形花圃,它的长比宽多10m,设花圃的宽为x m.则可列方程为( )
A.x (x﹣10)=200
B.2x+2 (x﹣10)=200
C.x(x+10)=200
D.2x+2(x+10)=200
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验室里,水平桌面上有甲、乙、丙三个相 同高度的圆柱形容器(容器足够高),底面半径之比为1:2:1,用两个相同的管子在10cm高度处连通(即管子底部离容器底10cm),现三个容器中,只有乙中有水,水位高4cm,如图所示.若每分钟同时向甲和丙注入相同量的水,开始注水1分钟,甲的水位上升3cm.则开始注入 分钟水量后,甲的水位比乙高1cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过∠AOB的平分线上一点C作CD∥OB交OA于点D,E是线段OC的中点,过点E作直线分别交射线CD,OB于点M,N,探究线段OD,ON,DM之间的数量关系,并证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com