
【题目】如图,抛物线y=ax2+bx(a≠0)的图象过原点O和点A(1, ![]() ),且与x轴交于点B,△AOB的面积为
),且与x轴交于点B,△AOB的面积为![]() 。
。
(1)求抛物线的解析式;
(2)若抛物线的对称轴上存在一点M,使△AOM的周长最小,求M点的坐标;
(3)点F是x轴上一动点,过F作x轴的垂线,交直线AB于点E,交抛物线于点P,且PE=![]() ,直接写出点E的坐标(写出符合条件的两个点即可)。
,直接写出点E的坐标(写出符合条件的两个点即可)。


【答案】(1)![]() ;(2)M(
;(2)M(![]() ,
, ![]() );(3)(下列四个中任意两个正确)(0,
);(3)(下列四个中任意两个正确)(0, ![]() )(
)(![]() ,
, ![]() )(
)(![]() ,
, ![]() )(
)(![]() ,
, ![]() )
)
【解析】试题分析:(1)由△AOB的面积得到OB的长,进而得出点B的坐标.再把A、B的坐标代入抛物线的解析式,解方程组即可得出结论;
(2)先求出抛物线的对称轴,由点B与点O关于对称轴对称,得到直线AB与对称轴的交点就是所要求的点M.由直线AB过A、B两点,得到直线AB的解析式,再求出直线AB和对称轴的交点即可;
(3)设F(x,0),表示出E,P的坐标,进而得到PE的长,解方程即可得出结论.
试题解析:解:(1)∵△AOB的面积为![]() , 点A(1,
, 点A(1, ![]() ),∴
),∴![]() =
=![]() ,∴OB=2,∴B(-2,0).∵抛物线过点A,B,∴
,∴OB=2,∴B(-2,0).∵抛物线过点A,B,∴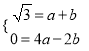 ,解得:
,解得: 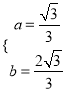 ,∴
,∴![]() ;
;
(2)抛物线的对称轴为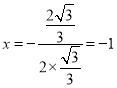 .∵点B与点O关于对称轴
.∵点B与点O关于对称轴![]() 对称,∴由题意得直线AB与对称轴的交点就是点M.设直线AB为:
对称,∴由题意得直线AB与对称轴的交点就是点M.设直线AB为: ![]() .∵直线AB过A、B两点,∴
.∵直线AB过A、B两点,∴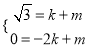 ,解得:
,解得:  ,∴
,∴![]() .
.
当![]() 时,
时, ![]() ,∴M(
,∴M(![]() ,
, ![]() );
);
(3)设F(x,0),则E(x, ![]() ),P(x,
),P(x, ![]() ),则PE=
),则PE= ,整理得:
,整理得: ![]() ,∴
,∴![]() 或
或![]() ,解得:x1=0,x2=-1,x3=
,解得:x1=0,x2=-1,x3=![]() ,x4=
,x4=![]() .∴E的坐标为(0,
.∴E的坐标为(0, ![]() )或(
)或(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() ).
).


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点.将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.
 试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
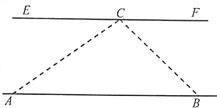
【题目】如图,湛河两岸AB与EF平行,小亮同学假期在湛河边A点处,测得对岸河边C处视线与湛河岸的夹角∠CAB=37°,沿河岸前行140米到点B处,测得对岸C处的视线与湛河岸夹角∠CBA=45°.问湛河的宽度约多少米?(参考数据:sin37°≈0.60,cos37°=0.80,tan37°=0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
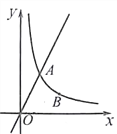
【题目】如图,直线y=2x与反比例函数![]() (k≠0,x>0)的图象交于点A(1,m),点B(n,t)是反比例函数图象上一点,且n=2t。
(k≠0,x>0)的图象交于点A(1,m),点B(n,t)是反比例函数图象上一点,且n=2t。
(1)求k的值和点B坐标;
(2)若点P在x轴上,使得△PAB的面积为2,直接写出点P坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点O是直线AB上一点,OC、OD为从点O引出的两条射线,∠BOD=30°,∠COD=![]() ∠AOC.
∠AOC.
(1)如图①,求∠AOC的度数;
(2)如图②,在∠AOD的内部作∠MON=90°,请直接写出∠AON与∠COM之间的数量关系 ;
(3)在(2)的条件下,若OM为∠BOC的角平分线,试说明∠AON=∠CON.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)1+(﹣1)+4﹣4
(2)﹣![]() ﹣(1﹣0.5)×
﹣(1﹣0.5)×![]() ×[1﹣(﹣2)2]
×[1﹣(﹣2)2]
(3)3x2y+xy2﹣3x2y﹣7xy2
(4)(5a﹣3b)﹣3(a﹣2b)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明购买了一套安居型商品房,他准备将地面铺上地砖,地面结构如图所示.请根据图中的数据(单位:m),解答下列问题:
(1)用含x、y的代数式表示地面总面积;
(2)若x=5,y=![]() ,铺1m2地砖的平均费用为80元,那么铺地砖的总费用为多少元?
,铺1m2地砖的平均费用为80元,那么铺地砖的总费用为多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
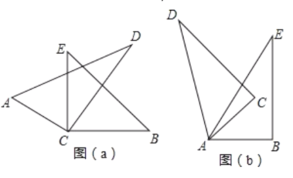
【题目】(1)如图(a),将一副三角尺(∠A=60°,∠B=45°)的直角顶点C叠放在一起,边CD与BE相交.
①若∠DCE=25°,则∠ACB=_____;若∠ACB=130°,则∠DCE= _____ ;
②猜想∠ACB与∠DCE的数量关系.直接写出答案,无需证明.
(2)如图(b),若两个相同的三角尺60°锐角的顶点A重合在一起, 边CD与A E相交,则∠DAB与∠CAE有何数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
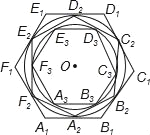
【题目】如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A11B11C11D11E11F11的边长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com