
【题目】已知,点O是直线AB上一点,OC、OD为从点O引出的两条射线,∠BOD=30°,∠COD=![]() ∠AOC.
∠AOC.
(1)如图①,求∠AOC的度数;
(2)如图②,在∠AOD的内部作∠MON=90°,请直接写出∠AON与∠COM之间的数量关系 ;
(3)在(2)的条件下,若OM为∠BOC的角平分线,试说明∠AON=∠CON.

【答案】(1)∠AOC=70°;(2)∠AON+20°=∠COM;(3)详见解析.
【解析】
(1)由题意可知:∠AOD=∠AOC+∠COD,即∠AOC+![]() ∠AOC=150°,求解即可;
∠AOC=150°,求解即可;
(2)由角的和差关系即可得出结论;
(3)OM是∠BOC的角平分线,可以求出∠CON=∠MON﹣∠COM=35°,而∠AON=∠AOC﹣∠CON=35°,即可得出结论.
(1)由题意可知:∠AOB=180°,∠BOD=30°,∠AOD=∠AOB﹣∠BOD=150°.
∵∠AOD=∠AOC+∠COD,∠COD=![]() ∠AOC,∴∠AOC+
∠AOC,∴∠AOC+![]() ∠AOC=150°,∴∠AOC=70°;
∠AOC=150°,∴∠AOC=70°;
(2)∵∠AOC=70°,∴∠AON+∠NOC=70°①.
∵∠MON=90°,∠MOC+∠NOC=90°②,由①②可得:∠AON+20°=∠COM;
(3)∵∠AOC=70°,∠AOB=180°,∴∠BOC=∠AOB﹣∠AOC=110°.
∵OM是∠BOC的角平分线,∴∠COM=![]() ∠BOC=55°.
∠BOC=55°.
∵∠MON=90°,∴∠CON=∠MON﹣∠COM=35°.
∵∠AOC=70°,∴∠AON=∠AOC﹣∠CON=35°,∴∠AON=∠CON.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】把下列各数分别填入相应的集合内:
﹣2.5,0,8,﹣2,![]() ,
,![]() , ﹣0.5252252225…(每两个5之间依次增加1个2).
, ﹣0.5252252225…(每两个5之间依次增加1个2).
(1)正数集合:{ …};
(2)负数集合:{ …};
(3)整数集合:{ …};
(4)无理数集合:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某重点中学校团委、学生会发出倡议,在初中各年级捐款购买书籍送给我市贫困地区的学校.初一年级利用捐款买甲、乙两种自然科学书籍若干本,用去5324元;初二年级买了A、B两种文学书籍若干本,用去4840元,其中A、B的数量分别与甲、乙的数量相等,且甲种书与B种书的单价相同,乙种书与A种书的单价相同.若甲、乙两种书的单价之和为121元,则初一和初二两个年级共向贫困地区的学校捐献了________本书.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】6张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
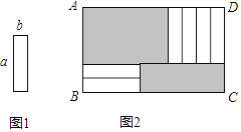
A. a=2b B. a=3b C. a=4b D. a=b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明一家利用国庆八天驾车到某景点旅游,小汽车出发前油箱有油35L,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图像回答下列问题:
(1)小汽车行驶______h后加油,中途加油_______L
(2)求加油前油箱余油量Q与行驶时间t的函数关系式
(3)如果小汽车在行驶过程中耗油量速度不变,加油站距景点200km,车速80km/h,要到达目的地,油箱中的油是否够用?请说明理由

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E, 
(1)求证:DE=DB;
(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y= ![]() 的图象经过点A(﹣1,2),则当x>1时,函数值y的取值范围是( )
的图象经过点A(﹣1,2),则当x>1时,函数值y的取值范围是( )
A.y>﹣1
B.﹣1<y<0
C.y<﹣2
D.﹣2<y<0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com