
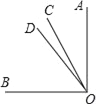
【题目】如图,已知∠AOB=90°,∠BOC比∠AOC大30°,OD是∠AOB的平分线,求∠COD的度数.
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】课题学习:设计概率模拟实验. 在学习概率时,老师说:“掷一枚质地均匀的硬币,大量重复实验后,正面朝上的概率约是 ![]() .”小海、小东、小英分别设计了下列三个模拟实验:
.”小海、小东、小英分别设计了下列三个模拟实验:
小海找来一个啤酒瓶盖(如图1)进行大量重复抛掷,然后计算瓶盖口朝上的次数与总次数的比值;
小东用硬纸片做了一个圆形转盘,转盘上分成8个大小一样的扇形区域,并依次标上1至8个数字(如图2),转动转盘10次,然后计算指针落在奇数区域的次数与总次数的比值;
小英在一个不透明的盒子里放了四枚除颜色外都相同的围棋子(如图3),其中有三枚是白子,一枚是黑子,从中随机同时摸出两枚棋子,并大量重复上述实验,然后计算摸出的两枚棋子颜色不同的次数与总次数的比值.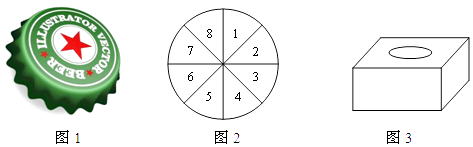
根据以上材料回答问题:
小海、小东、小英三人中,哪一位同学的实验设计比较合理,并简要说出其他两位同学实验的不足之处.
查看答案和解析>>
科目:初中数学 来源: 题型:
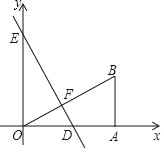
【题目】如图,Rt△AOB的顶点O与原点重合,直角顶点A在x轴上,顶点B的坐标为(4,3),直线y=﹣![]() x+4与x轴、y轴分别交于点D、E,交OB于点F.
x+4与x轴、y轴分别交于点D、E,交OB于点F.
(1)求点D、E两点的坐标及DE的长;
(2)写出图中的全等三角形及理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如同,△ABC内接于⊙O,且半径OC⊥AB,点D在半径OB的延长线上,且∠A=∠BCD=30°,AC=2,则由 ![]() ,线段CD和线段BD所围成图形的阴影部分的面积为 .
,线段CD和线段BD所围成图形的阴影部分的面积为 . 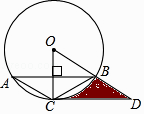
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地雪灾发生之后,灾区急需帐篷。某车间的甲、乙两名工人分别同时生产同种帐篷上的同种零件,他们一天生产零件y(个)与生产时间t(时)的函数关系如图所示。
①甲、乙中______先完成一天的生产任务;在生产过程中,______因机器故障停止生产______小时。
②当t=______时,甲、乙生产的零件个数相等。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AB是⊙O的直径,点P在CA的延长线上,∠CAD=45°.
(Ⅰ)若AB=4,求 ![]() 的长;
的长;
(Ⅱ)若 ![]() =
= ![]() ,AD=AP,求证:PD是⊙O的切线.
,AD=AP,求证:PD是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,两边及其中一边的对角分别对应相等的两个三角形不一定全等. 那么在什么情况下,它们会全等?
(1)阅读与证明:
对于这两个三角形均为直角三角形,显然它们全等.
对于这两个三角形均为钝角三角形,可证它们全等(证明略).
对于这两个三角形均为锐角三角形,它们也全等,可证明如下:
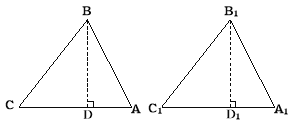
已知:△ABC、△A1B1C1均为锐角三角形,AB=A1B1,BC=B1C1,∠C=∠C1.
求证:△ABC≌△A1B1C1. (请你将下列证明过程补充完整)
证明:分别过点B,B1作BD⊥CA于D,B1D1⊥C1A1于D1.
则∠BDC=∠B1D1C1=90°,
∵BC=B1C1,∠C=∠C1,
∴△BCD≌△B1C1D1,
∴BD=B1D1.
______________________________。
(2)归纳与叙述:
由(1)可得到一个正确结论,请你写出这个结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点O是直线AB上一点,OC、OD为从点O引出的两条射线,∠BOD=30°,∠COD=![]() ∠AOC.
∠AOC.
(1)如图①,求∠AOC的度数;
(2)如图②,在∠AOD的内部作∠MON=90°,请直接写出∠AON与∠COM之间的数量关系 ;
(3)在(2)的条件下,若OM为∠BOC的角平分线,试说明∠AON=∠CON.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com