
【题目】如图,四边形ABCD内接于⊙O,AB是⊙O的直径,点P在CA的延长线上,∠CAD=45°.
(Ⅰ)若AB=4,求 ![]() 的长;
的长;
(Ⅱ)若 ![]() =
= ![]() ,AD=AP,求证:PD是⊙O的切线.
,AD=AP,求证:PD是⊙O的切线.
【答案】解:(Ⅰ)连接OC,OD, 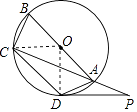
∵∠COD=2∠CAD,∠CAD=45°,
∴∠COD=90°,
∵AB=4,
∴OC= ![]() AB=2,
AB=2,
∴ ![]() 的长=
的长= ![]() ×π×2=π;
×π×2=π;
(Ⅱ)∵ ![]() =
= ![]() ,
,
∴∠BOC=∠AOD,
∵∠COD=90°,
∴∠AOD=45°,
∵OA=OD,
∴∠ODA=∠OAD,
∵∠AOD+∠ODA=∠OAD=180°,
∴∠ODA=67.5°,
∵AD=AP,
∴∠ADP=∠APD,
∵∠CAD=∠ADP+∠APD,∠CAD=45°,
∴∠ADP= ![]() CAD=22.5°,
CAD=22.5°,
∴∠ODP=∠ODA+∠ADP=90°,
∴PD是⊙O的切线.
【解析】(Ⅰ)连接OC,OD,由圆周角定理得到∠COD=2∠CAD,∠CAD=45°,于是得到∠COD=90°,根据弧长公式即可得到结论;(Ⅱ)由已知条件得到∠BOC=∠AOD,由圆周角定理得到∠AOD=45°,根据等腰三角形的性质得到∠ODA=∠OAD,求得∠ADP= ![]() CAD=22.5°,得到∠ODP=∠ODA+∠ADP=90°,于是得到结论.
CAD=22.5°,得到∠ODP=∠ODA+∠ADP=90°,于是得到结论.
【考点精析】根据题目的已知条件,利用圆内接四边形的性质和切线的判定定理的相关知识可以得到问题的答案,需要掌握把圆分成n(n≥3):1、依次连结各分点所得的多边形是这个圆的内接正n边形2、经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
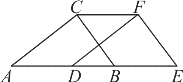
【题目】如图,在直角三角形ABC中,∠ACB=90°,AC=4cm,BC=3cm,将三角形ABC沿AB方向向右平移得到三角形DEF,若AE=8cm,DB=2cm.
(1)求三角形ABC向右平移的距离AD的长;
(2)求四边形AEFC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在不透明的袋子中装有3个红球和5个黄球,每个球除颜色外都相同,从中任意摸出一个球
(1)摸到哪种颜色球的可能性大?
(2)请你通过改变袋子中某一种颜色球的数量,设计一种方案;使“摸出红球”和“摸出黄球”的可能性大小相同.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求1+2+22+23+…+22018的值,可令S=1+2+22+23+…+22018,则2S=2+22+23+24+…22019,因此2S﹣S=22019﹣1,即S=22019﹣1.依照以上的方法,计算出1+5+52+53+…52017的值为( )
A. 52018﹣1 B. 52019﹣1 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索与发现:
(1)若直线a1⊥a2,a2∥a3,则直线a1与a3的位置关系是__________,请说明理由.
(2)若直线a1⊥a2,a2∥a3,a3⊥a4,则直线a1与a4的位置关系是________.(直接填结论,不需要证明)
(3)现在有2 011条直线a1,a2,a3,…,a2 011,且有a1⊥a2,a2∥a3,a3⊥a4,a4∥a5…,请你探索直线a1与a2 011的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.圆内接正六边形的边长与该圆的半径相等
B.在平面直角坐标系中,不同的坐标可以表示同一点
C.一元二次方程ax2+bx+c=0(a≠0)一定有实数根
D.将△ABC绕A点按顺时针方向旋转60°得△ADE,则△ABC与△ADE不全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】6张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
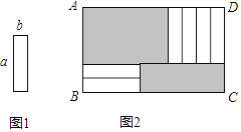
A. a=2b B. a=3b C. a=4b D. a=b
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com