
【题目】探索与发现:
(1)若直线a1⊥a2,a2∥a3,则直线a1与a3的位置关系是__________,请说明理由.
(2)若直线a1⊥a2,a2∥a3,a3⊥a4,则直线a1与a4的位置关系是________.(直接填结论,不需要证明)
(3)现在有2 011条直线a1,a2,a3,…,a2 011,且有a1⊥a2,a2∥a3,a3⊥a4,a4∥a5…,请你探索直线a1与a2 011的位置关系.
【答案】(1)a1⊥a3,理由详见解析;(2)a1∥a4;(3)a1⊥a2 011.
【解析】
(1)根据两直线平行,同位角相等得出相等的角,再根据垂直的定义解答;
(2)根据(1)中结论即可判定垂直;
(3)根据规律发现,与脚码是偶数的直线互相平行,与脚码是奇数的直线互相垂直,根据此规律即可判断.
(1)a1⊥a3.

理由如下:如图1,∵a1⊥a2,
∴∠1=90°,
∵a2∥a3,
∴∠2=∠1=90°,
∴a1⊥a3;
(2)同(1)的解法,如图2,直线a1与a4的位置关系是:a1∥a4;
(3)直线a1与a3的位置关系是:a1⊥a2⊥a3,
直线a1与a4的位置关系是:a1∥a4∥a5,
以四次为一个循环,⊥,⊥,∥,∥以此类推,a1∥a2009,a1⊥a2010,所以直线a1与a2011的位置关系是:a1⊥a2011.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:
【题目】为了给游客提供更好的服务,某景区随机对部分游客进行了关于“景区服务工作满意度”的调查,并根据调查结果绘制成如下不完整的统计图表.
满意度 | 人数 | 所占百分比 |
非常满意 | 12 | 10% |
满意 | 54 | m |
比较满意 | n | 40% |
不满意 | 6 | 5% |

根据图表信息,解答下列问题:
(1)本次调查的总人数为______,表中m的值为_______;
(2)请补全条形统计图;
(3)据统计,该景区平均每天接待游客约3600人,若将“非常满意”和“满意”作为游客对景区服务工作的肯定,请你估计该景区服务工作平均每天得到多少名游客的肯定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB=AC,D,E是BC边上的点,将△ABD绕点A旋转,得到△ACD',连接D'E.

(1)如图①,当∠BAC=120°,∠DAE=60°时,求证DE=D'E.
(2)如图②,当DE=D'E时,∠DAE与∠BAC有怎样的数量关系?请写出,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从一副扑克牌中取出方块3、红心6、黑挑10共三张牌,洗匀后正面朝下放在桌面上,小明和小丽玩摸牌游戏,游戏规则如下:先由小明随机摸出一张牌,记下牌面数字后放回,洗匀后正面朝下,再由小丽随机摸出一张牌,记下牌面数字、这样记为一次游戏.当两人摸出的牌面数字不同时,牌面数字大的获胜;当两人摸出的牌面数字相同,则为平局. 
(1)用画树状图或列表法,列出小明、小丽两人一次游戏的所有可能的结果.
(2)求小明获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,因为直线AB、CD相交于点P,AB∥EF,所以CD不平行于EF(________________________________________________________);
(2)因为直线a∥b,b∥c,所以a∥c(________________________________).
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
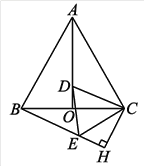
【题目】在等边△ABC中,AO是高,D为AO上一点,以CD为一边,在CD下方作等边△CDE,连接BE.
(1)求证:AD=BE;
(2)过点C作CH⊥BE,交BE的延长线于H,若BC=8,求CH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
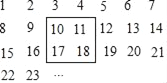
【题目】把正整数1,2,3,4,…排列成如图所示的一个表.
(1)用一正方形在表中随意框住4个数,把其中最大的数记为x,另三个数用含x的式子表示出来,从大到小依次是 , , ;
(2)在(1)的前提下,当被框住的4个数之和等于984时,x位于该表的第几行第几列?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料
小明遇到这样一个问题:求计算![]() 所得多项式的一次项系数.
所得多项式的一次项系数.
小明想通过计算![]() 所得的多项式解决上面的问题,但感觉有些繁琐,他想探寻一下,是否有相对简洁的方法.
所得的多项式解决上面的问题,但感觉有些繁琐,他想探寻一下,是否有相对简洁的方法.
他决定从简单情况开始,先找![]() 所得多项式中的一次项系数.通过观察发现:
所得多项式中的一次项系数.通过观察发现:
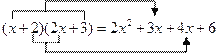
也就是说,只需用![]() 中的一次项系数1乘以
中的一次项系数1乘以![]() 中的常数项3,再用
中的常数项3,再用![]() 中的常数项2乘以
中的常数项2乘以![]() 中的一次项系数2,两个积相加
中的一次项系数2,两个积相加![]() ,即可得到一次项系数.
,即可得到一次项系数.
延续上面的方法,求计算![]() 所得多项式的一次项系数.可以先用
所得多项式的一次项系数.可以先用![]() 的一次项系数1,
的一次项系数1, ![]() 的常数项3,
的常数项3, ![]() 的常数项4,相乘得到12;再用
的常数项4,相乘得到12;再用![]() 的一次项系数2,
的一次项系数2, ![]() 的常数项2,
的常数项2, ![]() 的常数项4,相乘得到16;然后用
的常数项4,相乘得到16;然后用![]() 的一次项系数3,
的一次项系数3, ![]() 的常数项2,
的常数项2, ![]() 的常数项3,相乘得到18.最后将12,16,18相加,得到的一次项系数为46.
的常数项3,相乘得到18.最后将12,16,18相加,得到的一次项系数为46.
参考小明思考问题的方法,解决下列问题:
(1)计算![]() 所得多项式的一次项系数为 .
所得多项式的一次项系数为 .
(2)计算![]() 所得多项式的一次项系数为 .
所得多项式的一次项系数为 .
(3)若计算![]() 所得多项式的一次项系数为0,则
所得多项式的一次项系数为0,则![]() =_________.
=_________.
(4)若![]() 是
是![]() 的一个因式,则
的一个因式,则![]() 的值为 .
的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com