
【题目】阅读材料
小明遇到这样一个问题:求计算![]() 所得多项式的一次项系数.
所得多项式的一次项系数.
小明想通过计算![]() 所得的多项式解决上面的问题,但感觉有些繁琐,他想探寻一下,是否有相对简洁的方法.
所得的多项式解决上面的问题,但感觉有些繁琐,他想探寻一下,是否有相对简洁的方法.
他决定从简单情况开始,先找![]() 所得多项式中的一次项系数.通过观察发现:
所得多项式中的一次项系数.通过观察发现:
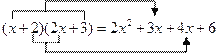
也就是说,只需用![]() 中的一次项系数1乘以
中的一次项系数1乘以![]() 中的常数项3,再用
中的常数项3,再用![]() 中的常数项2乘以
中的常数项2乘以![]() 中的一次项系数2,两个积相加
中的一次项系数2,两个积相加![]() ,即可得到一次项系数.
,即可得到一次项系数.
延续上面的方法,求计算![]() 所得多项式的一次项系数.可以先用
所得多项式的一次项系数.可以先用![]() 的一次项系数1,
的一次项系数1, ![]() 的常数项3,
的常数项3, ![]() 的常数项4,相乘得到12;再用
的常数项4,相乘得到12;再用![]() 的一次项系数2,
的一次项系数2, ![]() 的常数项2,
的常数项2, ![]() 的常数项4,相乘得到16;然后用
的常数项4,相乘得到16;然后用![]() 的一次项系数3,
的一次项系数3, ![]() 的常数项2,
的常数项2, ![]() 的常数项3,相乘得到18.最后将12,16,18相加,得到的一次项系数为46.
的常数项3,相乘得到18.最后将12,16,18相加,得到的一次项系数为46.
参考小明思考问题的方法,解决下列问题:
(1)计算![]() 所得多项式的一次项系数为 .
所得多项式的一次项系数为 .
(2)计算![]() 所得多项式的一次项系数为 .
所得多项式的一次项系数为 .
(3)若计算![]() 所得多项式的一次项系数为0,则
所得多项式的一次项系数为0,则![]() =_________.
=_________.
(4)若![]() 是
是![]() 的一个因式,则
的一个因式,则![]() 的值为 .
的值为 .
【答案】(1)7(2)-7(3)-3(4)-15
【解析】试题分析:(1)用2x+1中的一次项系数2乘以3x+2中的常数项2得4,用2x+1中的常数项1乘以3x+2中的一次项系数3得3,4+3=7即为积中一次项的系数;
(2)用x+1中的一次项系数1,3x+2中的常数项2,4x-3中的常数项-3相乘得-6,用x+1中的常数项1,3x+2中的一次项系数3,4x-3中的常数项-3相乘得-9,用x+1中的常数项1,3x+2中的常数项2,4x-3中的一次项系数4相乘得8,-6-9+8=-7即为积中一次项系数;
(3)用每一个因式中的一次项系数与另两个因式中的常数项相乘,再把所得的积相加,列方程、解方程即可得;
(4)设![]() 可以分成(
可以分成(![]() )(x2+kx+2),根据小明的算法则有k-3=0,a=-3k+2+1,b=-3×2+k,解方程即可得.
)(x2+kx+2),根据小明的算法则有k-3=0,a=-3k+2+1,b=-3×2+k,解方程即可得.
试题解析:(1)2×2+1×3=7,
故答案为:7;
(2)1×2×(-3)+3×1×(-3)+4×1×2=-7,
故答案为:-7;
(3)由题意得:1×a×(-1)+(-3)×1×(-1)+2×1×a=0,解得:a=-3,
故答案为:-3;
(4)设![]() 可以分成(
可以分成(![]() )(x2+kx+2),
)(x2+kx+2),
则有k-3=0,a=-3k+2+1,b=-3×2+k,
解得:k=3,a=-6,b=-3,
所以2a+b=-15,
故答案为:-15.
b=3-6=-3


科目:初中数学 来源: 题型:
【题目】观察下列关于自然数的等式:
a1:32-12=8×1;
a2:52-32=8×2;
a3:72-52=8×3;……
根据上述规律解决下列问题:
⑴写出第a4个等式:___________;
⑵写出你猜想的第an个等式(用含n的式子表示),并验证其正确性;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点P(1,0).点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位至点P3,第4次向右跳动3个单位至点P4,第5次又向上跳动1个单位至点P5,第6次向左跳动4个单位至点P6,…….照此规律,点P第100次跳动至点P100的坐标是( )

A. (-26,50) B. (-25,50) C. (26,50) D. (25,50)
查看答案和解析>>
科目:初中数学 来源: 题型:
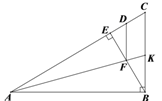
【题目】如图,在△ABC中,∠ABC=90°,BE⊥AC于点E,点D在AC上,且AD=AB,AK平分∠CAB,交线段BE于点F,交边CB于点K.
(1)在图中找出一对全等三角形,并证明;
(2)求证:FD∥BC .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,沿∠BAC的平分线AB1折叠,剪掉重叠部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重叠部分;…;将余下部分沿∠BnAnC的平分线AnBn+1折叠,点Bn与点C重合.无论折叠多少次,只要最后一次恰好重合,我们就称∠BAC是△ABC的好角.
小丽展示了确定∠BAC是△ABC的好角的两种情形.情形一:如图2,沿等腰三角形ABC顶角∠BAC的平分线AB1折叠,点B与点C重合;情形二:如图3,沿△ABC的∠BAC的平分线AB1折叠,剪掉重叠部分;将余下部分沿∠B1A1C的平分线A1B2折叠,此时点B1与点C重合.
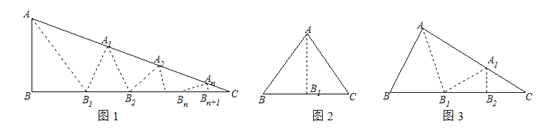
(1)小丽经过三次折叠发现了∠BAC是△ABC的好角,请探究∠B与∠C(不妨设∠B>∠C)之间的等量关系.
(2)根据以上内容猜想:若经过n次折叠∠BAC是△ABC的好角,则∠B与∠C(不妨设∠B>∠C)之间的等量关系为 ;
(3)如果一个三角形的最小角是15°,且满足该三角形的三个角均是此三角形的好角,则此三角形另两个角的度数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于0,1以及真分数p,q,r,若p<q<r,我们称q为p和r的中间分数.为了帮助我们找中间分数,制作了下表:
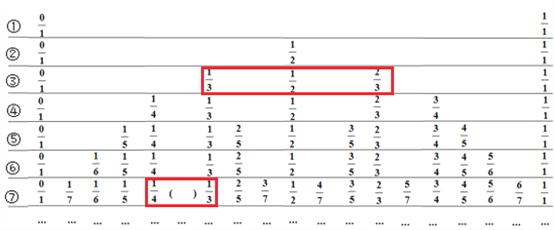
两个不等的正分数有无数多个中间分数.例如:上表中第③行中的3个分数![]() 、
、![]() 、
、![]() ,有
,有![]() ,所以
,所以![]() 为
为![]() 和
和![]() 的一个中间分数,在表中还可以找到
的一个中间分数,在表中还可以找到![]() 和
和![]() 的中间分数
的中间分数![]() ,
, ![]() ,
, ![]() ,
, ![]() .把这个表一直写下去,可以找到
.把这个表一直写下去,可以找到![]() 和
和![]() 更多的中间分数.
更多的中间分数.
(1)按上表的排列规律,完成下面的填空:
①上表中括号内应填的数为 ;
②如果把上面的表一直写下去,那么表中第一个出现的![]() 和
和![]() 的中间分数是 ;
的中间分数是 ;
(2)写出分数![]() 和
和![]() (a、b、c、d均为正整数,
(a、b、c、d均为正整数, ![]() ,
, ![]() )的一个中间分数(用含a、b、c、d的式子表示),并证明;
)的一个中间分数(用含a、b、c、d的式子表示),并证明;
(3)若![]() 与
与![]() (m、n、s、 t均为正整数)都是
(m、n、s、 t均为正整数)都是![]() 和
和![]() 的中间分数,则
的中间分数,则![]() 的最小值为 .
的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家预测一种应季衬衫能畅销市场,就用13 200元购进了一批这种衬衫,面市后果然供不应求,商家又用28 800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完利润率不低于25%(不考虑其他因素),那么每件衬衫的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)若a是(-4)2的平方根,b的一个平方根是2,求式子a+b的立方根;
(2)实数a,b互为相反数,c,d互为倒数,x的绝对值为![]() ,求式子x2+(a+b+cd)x+
,求式子x2+(a+b+cd)x+![]() +
+![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com