
ЁОЬтФПЁПЖдгк0ЃЌ1вдМАецЗжЪ§pЃЌqЃЌrЃЌШєp<q<rЃЌЮвУЧГЦqЮЊpКЭrЕФжаМфЗжЪ§ЃЎЮЊСЫАяжњЮвУЧевжаМфЗжЪ§ЃЌжЦзїСЫЯТБэЃК
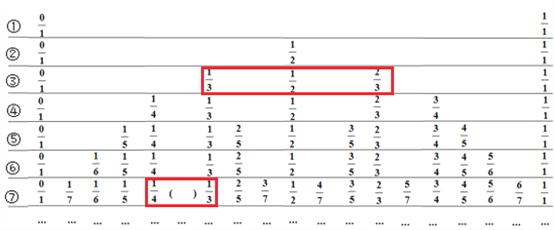
СНИіВЛЕШЕФе§ЗжЪ§гаЮоЪ§ЖрИіжаМфЗжЪ§ЃЎР§ШчЃКЩЯБэжаЕкЂлаажаЕФ3ИіЗжЪ§![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЌга
ЃЌга![]() ЃЌЫљвд
ЃЌЫљвд![]() ЮЊ
ЮЊ![]() КЭ
КЭ![]() ЕФвЛИіжаМфЗжЪ§ЃЌдкБэжаЛЙПЩвдевЕН
ЕФвЛИіжаМфЗжЪ§ЃЌдкБэжаЛЙПЩвдевЕН![]() КЭ
КЭ![]() ЕФжаМфЗжЪ§
ЕФжаМфЗжЪ§![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЎАбетИіБэвЛжБаДЯТШЅЃЌПЩвдевЕН
ЃЎАбетИіБэвЛжБаДЯТШЅЃЌПЩвдевЕН![]() КЭ
КЭ![]() ИќЖрЕФжаМфЗжЪ§ЃЎ
ИќЖрЕФжаМфЗжЪ§ЃЎ
ЃЈ1ЃЉАДЩЯБэЕФХХСаЙцТЩЃЌЭъГЩЯТУцЕФЬюПеЃК
ЂйЩЯБэжаРЈКХФкгІЬюЕФЪ§ЮЊ ЃЛ
ЂкШчЙћАбЩЯУцЕФБэвЛжБаДЯТШЅЃЌФЧУДБэжаЕквЛИіГіЯжЕФ![]() КЭ
КЭ![]() ЕФжаМфЗжЪ§ЪЧ ЃЛ
ЕФжаМфЗжЪ§ЪЧ ЃЛ
ЃЈ2ЃЉаДГіЗжЪ§![]() КЭ
КЭ![]() ЃЈaЁЂbЁЂcЁЂdОљЮЊе§ећЪ§ЃЌ
ЃЈaЁЂbЁЂcЁЂdОљЮЊе§ећЪ§ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЉЕФвЛИіжаМфЗжЪ§ЃЈгУКЌaЁЂbЁЂcЁЂdЕФЪНзгБэЪОЃЉЃЌВЂжЄУїЃЛ
ЃЉЕФвЛИіжаМфЗжЪ§ЃЈгУКЌaЁЂbЁЂcЁЂdЕФЪНзгБэЪОЃЉЃЌВЂжЄУїЃЛ
ЃЈ3ЃЉШє![]() гы
гы![]() ЃЈmЁЂnЁЂsЁЂ tОљЮЊе§ећЪ§ЃЉЖМЪЧ
ЃЈmЁЂnЁЂsЁЂ tОљЮЊе§ећЪ§ЃЉЖМЪЧ![]() КЭ
КЭ![]() ЕФжаМфЗжЪ§ЃЌдђ
ЕФжаМфЗжЪ§ЃЌдђ![]() ЕФзюаЁжЕЮЊ ЃЎ
ЕФзюаЁжЕЮЊ ЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂй![]() ЃЛЂк
ЃЛЂк![]() ЃЈ2ЃЉжЄУїМћНтЮіЃЈ3ЃЉ1504
ЃЈ2ЃЉжЄУїМћНтЮіЃЈ3ЃЉ1504
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЂйЙлВьУПвЛааЕФЙцТЩПЩЕУРЈКХЮЛгкЕкЂпааЃЌАДБэИёжаЕФЙцТЩПЩжЊЪЧ![]() ЃЛ
ЃЛ
ЂкЙлВьБэИёПЩжЊЕквЛИіГіЯжЕФ![]() КЭ
КЭ![]() ЕФжаМфЗжЪ§дкЕкЂрааЃЌЪЧ
ЕФжаМфЗжЪ§дкЕкЂрааЃЌЪЧ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉД№АИВЛЮЈвЛЃЌИљОнБэИёжаЙлВьЕНЕФЃЌПЩвдЮЊ![]() ЃЌЭЈЙ§ЭЦЕМжЄУїМДПЩЕУЃЛ
ЃЌЭЈЙ§ЭЦЕМжЄУїМДПЩЕУЃЛ
ЃЈ3ЃЉИљОнХХСаПЩжЊ![]() КЭ
КЭ![]() ЕФжаМфЗжЪ§га
ЕФжаМфЗжЪ§га![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЕШЃЌгЩДЫПЩЕУ.
ЕШЃЌгЩДЫПЩЕУ.
ЪдЬтНтЮіЃКЃЈ1ЃЉЂйЙлВьУПвЛааЕФЙцТЩПЩЕУРЈКХЮЛгкЕкЂпааЃЌАДЗжзгЕФХХађПЩжЊЪЧ![]() ЃЌ
ЃЌ
ЂкЙлВьБэИёПЩжЊЕквЛИіГіЯжЕФ![]() КЭ
КЭ![]() ЕФжаМфЗжЪ§дкЕкЂрааЃЌЪЧ
ЕФжаМфЗжЪ§дкЕкЂрааЃЌЪЧ![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊЃКЂй![]() ЃЛЂк
ЃЛЂк![]() ЃЎ
ЃЎ
ЃЈ2ЃЉБОЬтНсТлВЛЮЈвЛЃЌжЄЗЈВЛЮЈвЛЃЌШчЃК
НсТлЃК ![]() ЃЎ
ЃЎ
ЁпaЁЂbЁЂcЁЂdОљЮЊе§ећЪ§ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ
Ёр ЃЌ
ЃЌ
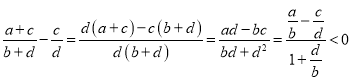 ЃЎ
ЃЎ
Ёр![]() ЃЎ
ЃЎ
ЃЈ3ЃЉИљОнХХСаПЩжЊ![]() КЭ
КЭ![]() ЕФжаМфЗжЪ§га
ЕФжаМфЗжЪ§га![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЕШЃЌгЩДЫПЩЕУmnЕФзюаЁжЕЮЊ1504ЃЌ
ЕШЃЌгЩДЫПЩЕУmnЕФзюаЁжЕЮЊ1504ЃЌ
ЙЪД№АИЮЊЃК1504.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
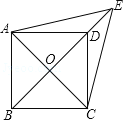
ЁОЬтФПЁПШчЭМЃЌвбжЊЦНааЫФБпаЮABCDжаЃЌЖдНЧЯпACЃЌBDНЛгкЕуOЃЌEЪЧBDбгГЄЯпЩЯЕФЕуЃЌЧвЁїACEЪЧЕШБпШ§НЧаЮЃЎ
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮABCDЪЧСтаЮЃЛ
ЃЈ2ЃЉШєЁЯAED=2ЁЯEADЃЌЧѓжЄЃКЫФБпаЮABCDЪЧе§ЗНаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌCNЪЧЕШБпЁї![]() ЕФЭтНЧ
ЕФЭтНЧ![]() ФкВПЕФвЛЬѕЩфЯпЃЌЕуAЙигкCNЕФЖдГЦЕуЮЊDЃЌСЌНгADЃЌBDЃЌCDЃЌЦфжаADЃЌBDЗжБ№НЛЩфЯпCNгкЕуEЃЌPЃЎ
ФкВПЕФвЛЬѕЩфЯпЃЌЕуAЙигкCNЕФЖдГЦЕуЮЊDЃЌСЌНгADЃЌBDЃЌCDЃЌЦфжаADЃЌBDЗжБ№НЛЩфЯпCNгкЕуEЃЌPЃЎ
ЃЈ1ЃЉвРЬтвтВЙШЋЭМаЮЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФДѓаЁЃЈгУКЌ
ЕФДѓаЁЃЈгУКЌ![]() ЕФЪНзгБэЪОЃЉЃЛ
ЕФЪНзгБэЪОЃЉЃЛ
ЃЈ3ЃЉгУЕШЪНБэЪОЯпЖЮ![]() ЃЌ
ЃЌ ![]() гы
гы![]() жЎМфЕФЪ§СПЙиЯЕЃЌВЂжЄУїЃЎ
жЎМфЕФЪ§СПЙиЯЕЃЌВЂжЄУїЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСВФСЯ
аЁУїгіЕНетбљвЛИіЮЪЬтЃКЧѓМЦЫу![]() ЫљЕУЖрЯюЪНЕФвЛДЮЯюЯЕЪ§ЃЎ
ЫљЕУЖрЯюЪНЕФвЛДЮЯюЯЕЪ§ЃЎ
аЁУїЯыЭЈЙ§МЦЫу![]() ЫљЕУЕФЖрЯюЪННтОіЩЯУцЕФЮЪЬтЃЌЕЋИаОѕгааЉЗБЫіЃЌЫћЯыЬНбАвЛЯТЃЌЪЧЗёгаЯрЖдМђНрЕФЗНЗЈЃЎ
ЫљЕУЕФЖрЯюЪННтОіЩЯУцЕФЮЪЬтЃЌЕЋИаОѕгааЉЗБЫіЃЌЫћЯыЬНбАвЛЯТЃЌЪЧЗёгаЯрЖдМђНрЕФЗНЗЈЃЎ
ЫћОіЖЈДгМђЕЅЧщПіПЊЪМЃЌЯШев![]() ЫљЕУЖрЯюЪНжаЕФвЛДЮЯюЯЕЪ§ЃЎЭЈЙ§ЙлВьЗЂЯжЃК
ЫљЕУЖрЯюЪНжаЕФвЛДЮЯюЯЕЪ§ЃЎЭЈЙ§ЙлВьЗЂЯжЃК
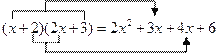
вВОЭЪЧЫЕЃЌжЛашгУ![]() жаЕФвЛДЮЯюЯЕЪ§1ГЫвд
жаЕФвЛДЮЯюЯЕЪ§1ГЫвд![]() жаЕФГЃЪ§Яю3ЃЌдйгУ
жаЕФГЃЪ§Яю3ЃЌдйгУ![]() жаЕФГЃЪ§Яю2ГЫвд
жаЕФГЃЪ§Яю2ГЫвд![]() жаЕФвЛДЮЯюЯЕЪ§2ЃЌСНИіЛ§ЯрМг
жаЕФвЛДЮЯюЯЕЪ§2ЃЌСНИіЛ§ЯрМг![]() ЃЌМДПЩЕУЕНвЛДЮЯюЯЕЪ§ЃЎ
ЃЌМДПЩЕУЕНвЛДЮЯюЯЕЪ§ЃЎ
бгајЩЯУцЕФЗНЗЈЃЌЧѓМЦЫу![]() ЫљЕУЖрЯюЪНЕФвЛДЮЯюЯЕЪ§ЃЎПЩвдЯШгУ
ЫљЕУЖрЯюЪНЕФвЛДЮЯюЯЕЪ§ЃЎПЩвдЯШгУ![]() ЕФвЛДЮЯюЯЕЪ§1ЃЌ
ЕФвЛДЮЯюЯЕЪ§1ЃЌ ![]() ЕФГЃЪ§Яю3ЃЌ
ЕФГЃЪ§Яю3ЃЌ ![]() ЕФГЃЪ§Яю4ЃЌЯрГЫЕУЕН12ЃЛдйгУ
ЕФГЃЪ§Яю4ЃЌЯрГЫЕУЕН12ЃЛдйгУ![]() ЕФвЛДЮЯюЯЕЪ§2ЃЌ
ЕФвЛДЮЯюЯЕЪ§2ЃЌ ![]() ЕФГЃЪ§Яю2ЃЌ
ЕФГЃЪ§Яю2ЃЌ ![]() ЕФГЃЪ§Яю4ЃЌЯрГЫЕУЕН16ЃЛШЛКѓгУ
ЕФГЃЪ§Яю4ЃЌЯрГЫЕУЕН16ЃЛШЛКѓгУ![]() ЕФвЛДЮЯюЯЕЪ§3ЃЌ
ЕФвЛДЮЯюЯЕЪ§3ЃЌ ![]() ЕФГЃЪ§Яю2ЃЌ
ЕФГЃЪ§Яю2ЃЌ ![]() ЕФГЃЪ§Яю3ЃЌЯрГЫЕУЕН18ЃЎзюКѓНЋ12ЃЌ16ЃЌ18ЯрМгЃЌЕУЕНЕФвЛДЮЯюЯЕЪ§ЮЊ46ЃЎ
ЕФГЃЪ§Яю3ЃЌЯрГЫЕУЕН18ЃЎзюКѓНЋ12ЃЌ16ЃЌ18ЯрМгЃЌЕУЕНЕФвЛДЮЯюЯЕЪ§ЮЊ46ЃЎ
ВЮПМаЁУїЫМПМЮЪЬтЕФЗНЗЈЃЌНтОіЯТСаЮЪЬтЃК
ЃЈ1ЃЉМЦЫу![]() ЫљЕУЖрЯюЪНЕФвЛДЮЯюЯЕЪ§ЮЊ ЃЎ
ЫљЕУЖрЯюЪНЕФвЛДЮЯюЯЕЪ§ЮЊ ЃЎ
ЃЈ2ЃЉМЦЫу![]() ЫљЕУЖрЯюЪНЕФвЛДЮЯюЯЕЪ§ЮЊ ЃЎ
ЫљЕУЖрЯюЪНЕФвЛДЮЯюЯЕЪ§ЮЊ ЃЎ
ЃЈ3ЃЉШєМЦЫу![]() ЫљЕУЖрЯюЪНЕФвЛДЮЯюЯЕЪ§ЮЊ0ЃЌдђ
ЫљЕУЖрЯюЪНЕФвЛДЮЯюЯЕЪ§ЮЊ0ЃЌдђ![]() =_________ЃЎ
=_________ЃЎ
ЃЈ4ЃЉШє![]() ЪЧ
ЪЧ![]() ЕФвЛИівђЪНЃЌдђ
ЕФвЛИівђЪНЃЌдђ![]() ЕФжЕЮЊ ЃЎ
ЕФжЕЮЊ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
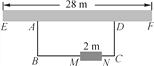
ЁОЬтФПЁПШчЭМЃЌРћгУвЛУцЧН(ЧНEFзюГЄПЩРћгУ28Уз)ЃЌЮЇГЩвЛИіОиаЮЛЈдАABCD.гыЧНЦНааЕФвЛБпBCЩЯвЊдЄСє2УзПэЕФШыПк(ШчЭМжаMNЫљЪОЃЌВЛгУЦіЧН)ЃЎЯжгаЦі60УзГЄЕФЧНЕФВФСЯЃЎ
(1)ЕБОиаЮЕФГЄBCЮЊЖрЩйУзЪБЃЌОиаЮЛЈдАЕФУцЛ§ЮЊ300ЦНЗНУзЃЛ
(2)ФмЗёЮЇГЩ480ЦНЗНУзЕФОиаЮЛЈдАЃЌЮЊЪВУДЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
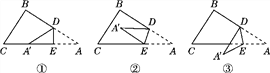
ЁОЬтФПЁПЁїABCЪЧвЛИіШ§НЧаЮЕФжНЦЌЃЌЕуDЃЌEЗжБ№ЪЧЁїABCБпABЃЌACЩЯЕФСНЕуЃЎ
(1)ШчЭМЂйЃЌШчЙћбижБЯпDEелЕўЃЌдђЁЯBDAЁфгыЁЯAЕФЙиЯЕЪЧ____________ЃЛ
(2)ШчЙћелГЩЭМЂкЕФаЮзДЃЌВТЯыЁЯBDAЁфЃЌЁЯCEAЁфКЭЁЯAЕФЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
(3)ШчЙћелГЩЭМЂлЕФаЮзДЃЌВТЯыЁЯBDAЁфЃЌЁЯCEAЁфКЭЁЯAЕФЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
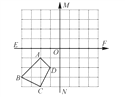
ЁОЬтФПЁП(ЦыЦыЙўЖћжаПМ)ШчЭМЫљЪОЃЌдкЫФБпаЮABCDжа.
(1)ЛГіЫФБпаЮA1B1C1D1ЃЌЪЙЫФБпаЮA1B1C1D1гыЫФБпаЮABCDЙигкжБЯпMNГЩжсЖдГЦЃЛ
(2)ЛГіЫФБпаЮA2B2C2D2ЃЌЪЙЫФБпаЮA2B2C2D2гыЫФБпаЮABCDЙигкЕуOжааФЖдГЦ.
(3)ЫФБпаЮA1B1C1D1гыЫФБпаЮA2B2C2D2ЪЧЗёЖдГЦЃЌШєЖдГЦЧыдкЭМжаЛГіЖдГЦжсЛђЖдГЦжааФ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
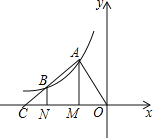
ЁОЬтФПЁПШчЭМЃЌЕуAЁЂBдкЗДБШР§КЏЪ§y=![]() ЕФЭМЯѓЩЯЃЌЙ§ЕуAЁЂBзїxжсЕФДЙЯпЃЌДЙзуЗжБ№ЪЧMЁЂNЃЌЩфЯпABНЛxжсгкЕуCЃЌШєOM=MN=NCЃЌЫФБпаЮAMNBЕФУцЛ§ЪЧ3ЃЌдђkЕФжЕЮЊЃЈ ЃЉ
ЕФЭМЯѓЩЯЃЌЙ§ЕуAЁЂBзїxжсЕФДЙЯпЃЌДЙзуЗжБ№ЪЧMЁЂNЃЌЩфЯпABНЛxжсгкЕуCЃЌШєOM=MN=NCЃЌЫФБпаЮAMNBЕФУцЛ§ЪЧ3ЃЌдђkЕФжЕЮЊЃЈ ЃЉ
AЃЎ2 BЃЎ4 CЃЎЉ2 DЃЎЉ4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЗНИёжНФкНЋЁїABCЫЎЦНЯђгвЦНвЦ4ИіЕЅЮЛЕУЕНЁїAЁфBЁфCЁфЃЎ

ЃЈ1ЃЉВЙШЋЁїAЁфBЁфCЁфЃЌРћгУЭјИёЕуКЭжБГпЛЭМЃЛ
ЃЈ2ЃЉЭМжаACгыA1C1ЕФЙиЯЕЪЧЃК______ЃЛ
ЃЈ3ЃЉЛГіЁїABCжаABБпЩЯЕФжаЯпCEЃЛ
ЃЈ4ЃЉЦНвЦЙ§ГЬжаЃЌЯпЖЮACЩЈЙ§ЕФУцЛ§ЪЧ_________
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com