【题目】把下列各数分别填入相应的集合内：
﹣2.5，0，8，﹣2，
，
， ﹣0.5252252225…（每两个5之间依次增加1个2）．
（1）正数集合：{ …}；
（2）负数集合：{ …}；
（3）整数集合：{ …}；
（4）无理数集合：{ …}．
【答案】（1）正数集合：｛8，
，，
，…｝；
（2）负数集合：｛－2．5，－2 ，－0．525225222…，…｝；
（3）整数集合：｛0，8，－2 …｝；
（4）无理数集合：{，－0．5252252225…，…}．
【解析】
试题正数包括正有理数和正无理数，负数包括负有理数和负无理数，整数包括正整数、负整数和0，无理数是无限不循环小数.由此即可解决问题.
试题解析：
（1）正数集合：{8，
，…}；
（2）负数集合：{﹣2.5，﹣2，﹣0.5252252225…（每两个5之间依次增加1个2）…}；
（3）整数集合：{0，8，﹣2，…}；
（4）无理数集合：{
，﹣0.5252252225…（每两个5之间依次增加1个2），…}．
寒假乐园北京教育出版社系列答案科目：初中数学 来源： 题型：
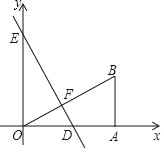
【题目】如图，Rt△AOB的顶点O与原点重合，直角顶点A在x轴上，顶点B的坐标为（4，3），直线y＝﹣
x+4与x轴、y轴分别交于点D、E，交OB于点F．
（1）求点D、E两点的坐标及DE的长；
（2）写出图中的全等三角形及理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们知道，两边及其中一边的对角分别对应相等的两个三角形不一定全等. 那么在什么情况下，它们会全等?
（1）阅读与证明：
对于这两个三角形均为直角三角形，显然它们全等.
对于这两个三角形均为钝角三角形，可证它们全等（证明略）.
对于这两个三角形均为锐角三角形，它们也全等，可证明如下：
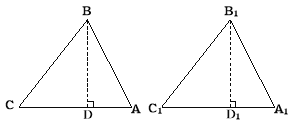
已知：△ABC、△A1B1C1均为锐角三角形，AB＝A1B1，BC＝B1C1，∠C＝∠C1.
求证：△ABC≌△A1B1C1. （请你将下列证明过程补充完整）
证明：分别过点B，B1作BD⊥CA于D，B1D1⊥C1A1于D1.
则∠BDC＝∠B1D1C1＝90°，
∵BC＝B1C1，∠C＝∠C1，
∴△BCD≌△B1C1D1，
∴BD＝B1D1.
______________________________。
（2）归纳与叙述：
由（1）可得到一个正确结论，请你写出这个结论.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB为⊙O的直径，CB，CD分别切⊙O于点B，D，CD交BA的延长线于点E，CO的延长线交⊙O于点G，EF⊥OG于点F．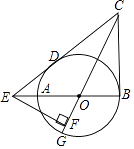 
（1）求证：∠FEB=∠ECF；
（2）若BC=6，DE=4，求EF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
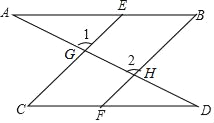
【题目】如图，一条直线分别与直线BE、直线CE、直线CF、直线BF相交于点A，G，D，H且∠1=∠2，∠B=∠C
（1）找出图中相互平行的线，说说它们之间为什么是平行的；
（2）证明：∠A=∠D．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点A是直线AM与⊙O的交点，点B在⊙O上，BD⊥AM垂足为D，BD与⊙O交于点C，OC平分∠AOB，∠B=60°．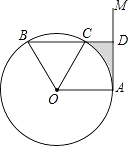
（1）求证：AM是⊙O的切线；
（2）若DC=2，求图中阴影部分的面积（结果保留π和根号）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，点O是直线AB上一点，OC、OD为从点O引出的两条射线，∠BOD=30°，∠COD=
∠AOC．
（1）如图①，求∠AOC的度数；
（2）如图②，在∠AOD的内部作∠MON=90°，请直接写出∠AON与∠COM之间的数量关系 ；
（3）在（2）的条件下，若OM为∠BOC的角平分线，试说明∠AON=∠CON．
查看答案和解析>>
科目：初中数学 来源： 题型：
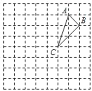
【题目】已知：如图，在边长为1的小正方形网格中，△ABC的顶点都在格点上，建立适当的平面直角坐标系xOy，使得点A、B的坐标分别为（2，3）、（3，2）．
（1）在网格中画出满足要求的平面直角坐标系，写出点C的坐标为 ；
（2）若点P是x轴上的一个动点，则PA+PB的最小值为 ．（直接写出结果）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
