
【题目】如图,AB为⊙O的直径,CB,CD分别切⊙O于点B,D,CD交BA的延长线于点E,CO的延长线交⊙O于点G,EF⊥OG于点F. 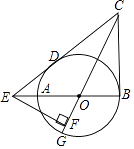
(1)求证:∠FEB=∠ECF;
(2)若BC=6,DE=4,求EF的长.
【答案】
(1)证明:∵CB,CD分别切⊙O于点B,D,
∴OC平分∠BCE,即∠ECO=∠BCO,OB⊥BC,
∴∠BCO+∠COB=90°,
∵EF⊥OG,
∴∠FEB+∠FOE=90°,
而∠COB=∠FOE,
∴∠FEB=∠ECF;
(2)解:连接OD,如图,
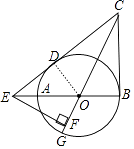
∵CB,CD分别切⊙O于点B,D,
∴CD=CB=6,OD⊥CE,
∴CE=CD+DE=6+4=10,
在Rt△BCE中,BE= ![]() =8,
=8,
设⊙O的半径为r,则OD=OB=r,OE=8﹣r,
在Rt△ODE中,r2+42=(8﹣r)2,解得r=3,
∴OE=8﹣3=5,
在Rt△OBC中,OC= ![]() =3
=3 ![]() ,
,
∵∠COB=∠FOE,
∴△OEF∽△OCB,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴EF=2 ![]() .
.
【解析】(1)利用切线长定理得到OC平分∠BCE,即∠ECO=∠BCO,利用切线的性质得OB⊥BC,则∠BCO+∠COB=90°,由于∠FEB+∠FOE=90°,∠COB=∠FOE,所以∠FEB=∠ECF;(2)连接OD,如图,利用切线长定理和切线的性质得到CD=CB=6,OD⊥CE,则CE=10,利用勾股定理可计算出BE=8,设⊙O的半径为r,则OD=OB=r,OE=8﹣r,在Rt△ODE中,根据勾股定理得r2+42=(8﹣r)2 , 解得r=3,所以OE=5,OC=3 ![]() ,然后证明△OEF∽△OCB,利用相似比可计算出EF的长.
,然后证明△OEF∽△OCB,利用相似比可计算出EF的长.
【考点精析】认真审题,首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2),还要掌握垂径定理(垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b的图象如图所示,
(1)求出这个函数关系式.
(2)图象上有一点P(4,m),求m的值.
(3)判断点(﹣4,3)和 (6,﹣6)是否在此直线上.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知EF∥GH,A、D为GH上的两点,M、B为EF上的两点,延长AM于点C,AB平分∠DAC,直线DB平分∠FBC,若∠ACB=100°,则∠DBA的度数为________.
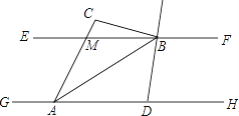
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数分别填入相应的集合内:
﹣2.5,0,8,﹣2,![]() ,
,![]() , ﹣0.5252252225…(每两个5之间依次增加1个2).
, ﹣0.5252252225…(每两个5之间依次增加1个2).
(1)正数集合:{ …};
(2)负数集合:{ …};
(3)整数集合:{ …};
(4)无理数集合:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某重点中学校团委、学生会发出倡议,在初中各年级捐款购买书籍送给我市贫困地区的学校.初一年级利用捐款买甲、乙两种自然科学书籍若干本,用去5324元;初二年级买了A、B两种文学书籍若干本,用去4840元,其中A、B的数量分别与甲、乙的数量相等,且甲种书与B种书的单价相同,乙种书与A种书的单价相同.若甲、乙两种书的单价之和为121元,则初一和初二两个年级共向贫困地区的学校捐献了________本书.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司到果园基地购买某种优质水果,慰问医务工作者,果园基地对购买量在3000千克以上(含3000千克)的有两种销售方案,甲方案:每千克9元,由基地送货上门.乙方案:每千克8元,由顾客自己租车运回,已知该公司租车从基地到公司的运输费为5000元.
(1)分别写出该公司两种购买方案的付款y(元)与所购买的水果质量x(千克)之间的函数关系式,并写出自变量x的取值范围.
(2)依据购买量判断,选择哪种购买方案付款最少?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com