
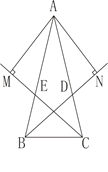
【题目】如图所示,在△ABC中,AB﹦AC,BD、CE分别是所在角的平分线,AN⊥BD于N点,AM⊥CE于M点。求证:AM﹦AN
科目:初中数学 来源: 题型:
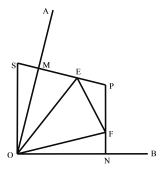
【题目】⑴如图1,点M、N分别在∠AOB的边OA、OB上,且OM=ON,过点M、N分别作MP⊥OA、NP⊥OB,MP、NP交于P,E、F分别为线段MP、NP上的点,且∠EOF=![]() ∠AOB,延长PM到S,使MS=NF,连接OS,则∠EOF与∠EOS的数量关系为 ,线段NF、EM、EF的数量关系为
∠AOB,延长PM到S,使MS=NF,连接OS,则∠EOF与∠EOS的数量关系为 ,线段NF、EM、EF的数量关系为
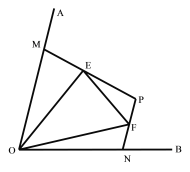
⑵如图2,点M、N分别在∠AOB的边OA、OB上,且OM=ON,![]() , E、F分别为线段MP、NP上的点,且∠EOF=
, E、F分别为线段MP、NP上的点,且∠EOF=![]() ∠AOB,⑴中的线段NF、EM、EF的数量关系是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明。
∠AOB,⑴中的线段NF、EM、EF的数量关系是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明。
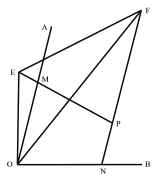
⑶如图3,点M、N分别在∠AOB的边OA、OB上,且OM=ON,![]() , E、F分别为线段PM、NP延长线上的点,且∠EOF=
, E、F分别为线段PM、NP延长线上的点,且∠EOF=![]() ∠AOB,⑴中的线段NF、EM、EF的数量关系是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明。
∠AOB,⑴中的线段NF、EM、EF的数量关系是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校八、九年级部分学生的睡眠情况,随机抽取了该校八、九年级部分学生进行调查,已知抽取的八年级与九年级的学生人数相同,利用抽样所得的数据绘制如图的统计图表:
睡眠情况分段情况如下
组别 | 睡眠时间x(小时) |
A | 4.5≤x<5.5 |
B | 5.5≤x<6.5 |
C | 6.5≤x<7.5 |
D | 7.5≤x<8.5 |
E | 8.5≤x<9.5 |
根据图表提供的信息,回答下列问题:
(Ⅰ)直接写出统计图中a的值 ![]()
(Ⅱ)睡眠时间少于6.5小时为严重睡眠不足,则从该校八、九年级各随机抽一名学生,被抽到的这两位学生睡眠严重不足的可能性分别有多大?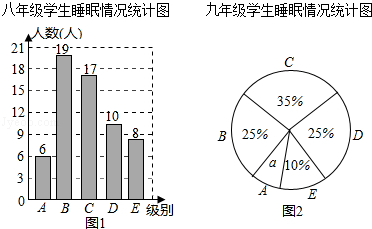
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地雪灾发生之后,灾区急需帐篷。某车间的甲、乙两名工人分别同时生产同种帐篷上的同种零件,他们一天生产零件y(个)与生产时间t(时)的函数关系如图所示。
①甲、乙中______先完成一天的生产任务;在生产过程中,______因机器故障停止生产______小时。
②当t=______时,甲、乙生产的零件个数相等。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,因为直线AB、CD相交于点P,AB∥EF,所以CD不平行于EF(________________________________________________________);
(2)因为直线a∥b,b∥c,所以a∥c(________________________________).
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,两边及其中一边的对角分别对应相等的两个三角形不一定全等. 那么在什么情况下,它们会全等?
(1)阅读与证明:
对于这两个三角形均为直角三角形,显然它们全等.
对于这两个三角形均为钝角三角形,可证它们全等(证明略).
对于这两个三角形均为锐角三角形,它们也全等,可证明如下:
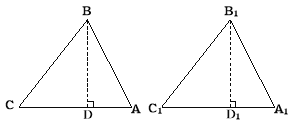
已知:△ABC、△A1B1C1均为锐角三角形,AB=A1B1,BC=B1C1,∠C=∠C1.
求证:△ABC≌△A1B1C1. (请你将下列证明过程补充完整)
证明:分别过点B,B1作BD⊥CA于D,B1D1⊥C1A1于D1.
则∠BDC=∠B1D1C1=90°,
∵BC=B1C1,∠C=∠C1,
∴△BCD≌△B1C1D1,
∴BD=B1D1.
______________________________。
(2)归纳与叙述:
由(1)可得到一个正确结论,请你写出这个结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习了二次根式的相关运算后,我们发现一些含有根号的式子可以表示成另一个式子的平方,如:
3+2![]() =2+2
=2+2![]() +1=(
+1=(![]() )2+2
)2+2![]() +1=(
+1=(![]() +1)2;
+1)2;
5+2![]() =2+2
=2+2![]() +3=(
+3=(![]() )2+2×
)2+2×![]() ×
×![]() +(
+(![]() )2=(
)2=(![]() +
+![]() )2
)2
(1)请仿照上面式子的变化过程,把下列各式化成另一个式子的平方的形式:
①4+2![]() ;②6+4
;②6+4![]()
(2)若a+4![]() =(m+n
=(m+n![]() )2,且a,m,n都是正整数,试求a的值.
)2,且a,m,n都是正整数,试求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,CB,CD分别切⊙O于点B,D,CD交BA的延长线于点E,CO的延长线交⊙O于点G,EF⊥OG于点F. 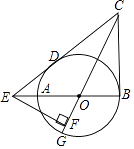
(1)求证:∠FEB=∠ECF;
(2)若BC=6,DE=4,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某重点中学校团委、学生会发出倡议,在初中各年级捐款购买书籍送给我市贫困地区的学校.初一年级利用捐款买甲、乙两种自然科学书籍若干本,用去5324元;初二年级买了A、B两种文学书籍若干本,用去4840元,其中A、B的数量分别与甲、乙的数量相等,且甲种书与B种书的单价相同,乙种书与A种书的单价相同.若甲、乙两种书的单价之和为121元,则初一和初二两个年级共向贫困地区的学校捐献了________本书.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com