
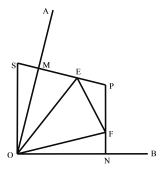
【题目】⑴如图1,点M、N分别在∠AOB的边OA、OB上,且OM=ON,过点M、N分别作MP⊥OA、NP⊥OB,MP、NP交于P,E、F分别为线段MP、NP上的点,且∠EOF=![]() ∠AOB,延长PM到S,使MS=NF,连接OS,则∠EOF与∠EOS的数量关系为 ,线段NF、EM、EF的数量关系为
∠AOB,延长PM到S,使MS=NF,连接OS,则∠EOF与∠EOS的数量关系为 ,线段NF、EM、EF的数量关系为
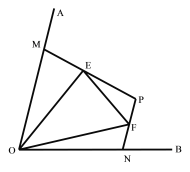
⑵如图2,点M、N分别在∠AOB的边OA、OB上,且OM=ON,![]() , E、F分别为线段MP、NP上的点,且∠EOF=
, E、F分别为线段MP、NP上的点,且∠EOF=![]() ∠AOB,⑴中的线段NF、EM、EF的数量关系是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明。
∠AOB,⑴中的线段NF、EM、EF的数量关系是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明。
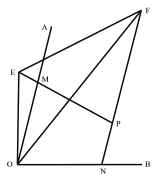
⑶如图3,点M、N分别在∠AOB的边OA、OB上,且OM=ON,![]() , E、F分别为线段PM、NP延长线上的点,且∠EOF=
, E、F分别为线段PM、NP延长线上的点,且∠EOF=![]() ∠AOB,⑴中的线段NF、EM、EF的数量关系是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明。
∠AOB,⑴中的线段NF、EM、EF的数量关系是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明。
【答案】(1)相等,EF=FN+EM;(2)见解析;(3)见解析.
【解析】
(1)结论:相等,EF=FN+EM.先证明△OMS≌△ONF,再证明△OES≌△OEF即可解决问题.
(2)结论:EF=FN+EM.如图2中,延长EM到S,使得SM=FN,连接SO,先证明△OMS≌△ONF,再证明△OES≌△OEF即可解决问题.
(3)结论:EF=FN-EM.如图3中,延长ME到S,使得MS=FN,连接SO,先证明△OMS≌△ONF,再证明△OES≌△OEF即可解决问题.
理由:如图1中,
在△OMS和△ONF中,OM=ON,∠OMS=∠ONF,MS=FN,
∴△OMS≌△ONF,
∴OS=OF,∠SOM=∠FON,
∵∠EOF=![]() ∠MON=∠EOM+∠FON=∠EOM+∠SOM=∠SOE,
∠MON=∠EOM+∠FON=∠EOM+∠SOM=∠SOE,
在△OES和△OEF中,OE=OE,∠SOE=∠EOF,OS=OF,
∴△OES≌△OEF,
∴EF=SE=SM+EM=FN+EM.
故答案为相等,EF=FN+EM.
(2)如图2中,延长EM到S,使得SM=FN,连接SO.

∵∠OMP+∠ONP=180°,∠OMS+∠OMP=180°,
∴∠OMS=∠ONF,
在△OMS和△ONF中,OM=ON,∠OMS=∠ONF,MS=FN,
∴△OMS≌△ONF,
∴OS=OF,∠SOM=∠FON,
∵∠EOF=![]() ∠MON=∠EOM+∠FON=∠EOM+∠SOM=∠SOE,
∠MON=∠EOM+∠FON=∠EOM+∠SOM=∠SOE,
在△OES和△OEF中,OE=OE,∠SOE=∠EOF,OS=OF,
∴△OES≌△OEF,
∴EF=SE=SM+EM=FN+EM.
(3)结论:EF=FN-EM.
理由:如图3中,延长ME到S,使得MS=FN,连接SO.

∵∠OMP+∠ONP=180°,∠OMS+∠OMP=180°,
∴∠OMS=∠ONF,
在△OMS和△ONF中,OM=ON,∠OMS=∠ONF,MS=FN∴△OMS≌△ONF,
∴OS=OF,∠SOM=∠FON,
∵∠EOF=![]() ∠MON=∠EOM+∠FON=∠EOM+∠SOM=∠SOE,
∠MON=∠EOM+∠FON=∠EOM+∠SOM=∠SOE,
在△OES和△OEF中,OE=OE,∠SOE=∠EOF,OS=OF,
∴△OES≌△OEF,
∴EF=SE=SM-EM=FN-EM.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1).一张透明纸上画有一个点和一条抛物线,平移透明纸,这个点与点A重合,此时抛物线的函数表达式为y=x2 , 再次平移透明纸,使这个点与点C重合,则该抛物线的函数表达式变为( )
A.y=x2+8x+14
B.y=x2-8x+14
C.y=x2+4x+3
D.y=x2-4x+3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果. 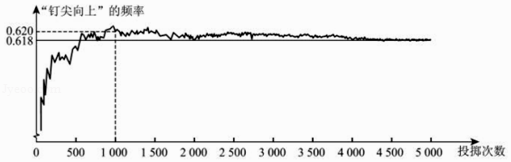
下面有三个推断:
①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的概率是0.616;
②随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;
③若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率一定是0.620.
其中合理的是( )
A.①
B.②
C.①②
D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.
(1)填空:与∠AOE互补的角有 ;
(2)若∠COD=30°,求∠DOE的度数;
(3)当∠AOD=α°时,请直接写出∠DOE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某公园里一处矩形风景欣赏区ABCD,长AB=50米,宽BC=25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为___________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
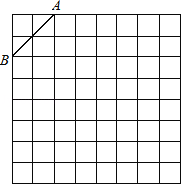
(1)在网格中建立平面直角坐标系,使A点坐标为(﹣2,4),B点坐标为(﹣4,2);
(2)在第二象限内的格点上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点坐标是________;
(3)△ABC的周长=_________(结果保留根号);
(4)画出△ABC关于关于y轴对称的△A′B′C′.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了增强学生体质,决定开设以下体育课外活动项目:A篮球、B乒乓球、C跳绳、D踢毽子,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题: 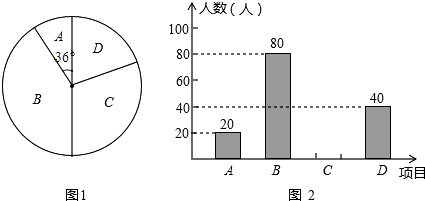
(1)这次被调查的学生共有人;
(2)请你将条形统计图补充完成;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b的图象如图所示,
(1)求出这个函数关系式.
(2)图象上有一点P(4,m),求m的值.
(3)判断点(﹣4,3)和 (6,﹣6)是否在此直线上.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com