
【题目】如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.
(1)填空:与∠AOE互补的角有 ;
(2)若∠COD=30°,求∠DOE的度数;
(3)当∠AOD=α°时,请直接写出∠DOE的度数.

【答案】(1)∠BOE、∠COE;(2)∠DOE=90°;(3)∠DOE=90°.
【解析】
(1)由图可知∠BOE是与∠AOE互补的角,又由射线OE平分∠BOC可知∠BOE=∠COE,则可知与∠AOE互补的角是∠BOE、∠COE;
(2)由射线OD平分∠AOC可求解出∠AOC的度数,继而利用互补可求解出∠BOC的度数,再由射线OE分别∠BOC,可求解出∠EOC的度数,则∠DOE=∠COD+∠COE;
(3)由射线OD和射线OE分别平分∠AOC和∠BOC,以及∠AOC和∠BOC互补可知∠DOE=![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() ×180°=90°.
×180°=90°.
解:(1)∵OE平分∠BOC,
∴∠BOE=∠COE;
∵∠AOE+∠BOE=180°,
∴∠AOE+∠COE=180°,
∴与∠AOE互补的角是∠BOE、∠COE;
故答案为∠BOE、∠COE;
(2)∵OD、OE分别平分∠AOC、∠BOC,
∴∠COD=∠AOD=30°,∠COE=∠BOE=![]() ∠BOC,
∠BOC,
∴∠AOC=2×30°=60°,
∴∠BOC=180°﹣60°=120°,
∴∠COE=![]() ∠BOC=60°,
∠BOC=60°,
∴∠DOE=∠COD+∠COE=90°;
(3)由由射线OD和射线OE分别平分∠AOC和∠BOC分别可得∠AOD=∠COD=![]() ∠AOC, ∠BOE=∠COE=
∠AOC, ∠BOE=∠COE=![]() ∠BOC,则∠DOE=∠COD+∠COE=
∠BOC,则∠DOE=∠COD+∠COE=![]() (∠AOC+∠BOC),再由图可知∠AOC和∠BOC互补,故∠DOE=
(∠AOC+∠BOC),再由图可知∠AOC和∠BOC互补,故∠DOE=![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() ×180°=90°,与α无关.
×180°=90°,与α无关.
故当∠AOD=α°时,∠DOE=90°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小龙在学校组织的社会调查活动中负责了解他所居住的小区450户居民的家庭收入情况. 他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.
分组 | 频数 | 百分比 |
600≤ | 2 | 5% |
800≤ | 6 | 15% |
1000≤ | 45% | |
9 | 22.5% | |
1600≤ | 2 | |
合计 | 40 | 100% |

根据以上提供的信息,解答下列问题:
(1)补全频数分布表.
(2)补全频数分布直方图.
(3)绘制相应的频数分布折线图.
(4)请你估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB=2,MN⊥AB于点M,且AM=BM,P是射线MN上一动点,E,D分别是PA,PB的中点,过点A,M,D的圆与BP的另一交点C(点C在线段BD上),连结AC,DE.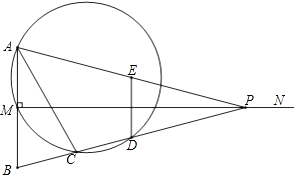
(1)当∠APB=28°时,求∠B和 ![]() 的度数;
的度数;
(2)求证:AC=AB.
(3)在点P的运动过程中
①当MP=4时,取四边形ACDE一边的两端点和线段MP上一点Q,若以这三点为顶点的三角形是直角三角形,且Q为锐角顶点,求所有满足条件的MQ的值;
②记AP与圆的另一个交点为F,将点F绕点D旋转90°得到点G,当点G恰好落在MN上时,连结AG,CG,DG,EG,直接写出△ACG和△DEG的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
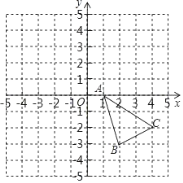
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(1,0),B(2,﹣3),C(4,﹣2).
(1)①画出△ABC关于x轴的对称图形△A1B1C1;②画出△A1B1C1向左平移3个单位长度后得到的△A2B2C2;
(2)如果AC上有一点P(m,n)经过上述两次变换,那么对应A2C2上的点P2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
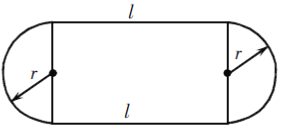
【题目】如图,操场的两端为半圆形,中间是一个长方形. 已知半圆的半径为r,直跑道的长为l,请用关于r,l的多项式表示这个操场的面积. 这个多项式能分解因式吗?若能,请把它分解因式,并计算当r=40m,l=30πm时操场的面积(结果保留π);若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课题学习:设计概率模拟实验. 在学习概率时,老师说:“掷一枚质地均匀的硬币,大量重复实验后,正面朝上的概率约是 ![]() .”小海、小东、小英分别设计了下列三个模拟实验:
.”小海、小东、小英分别设计了下列三个模拟实验:
小海找来一个啤酒瓶盖(如图1)进行大量重复抛掷,然后计算瓶盖口朝上的次数与总次数的比值;
小东用硬纸片做了一个圆形转盘,转盘上分成8个大小一样的扇形区域,并依次标上1至8个数字(如图2),转动转盘10次,然后计算指针落在奇数区域的次数与总次数的比值;
小英在一个不透明的盒子里放了四枚除颜色外都相同的围棋子(如图3),其中有三枚是白子,一枚是黑子,从中随机同时摸出两枚棋子,并大量重复上述实验,然后计算摸出的两枚棋子颜色不同的次数与总次数的比值.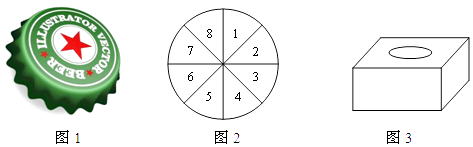
根据以上材料回答问题:
小海、小东、小英三人中,哪一位同学的实验设计比较合理,并简要说出其他两位同学实验的不足之处.
查看答案和解析>>
科目:初中数学 来源: 题型:
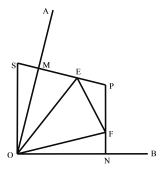
【题目】⑴如图1,点M、N分别在∠AOB的边OA、OB上,且OM=ON,过点M、N分别作MP⊥OA、NP⊥OB,MP、NP交于P,E、F分别为线段MP、NP上的点,且∠EOF=![]() ∠AOB,延长PM到S,使MS=NF,连接OS,则∠EOF与∠EOS的数量关系为 ,线段NF、EM、EF的数量关系为
∠AOB,延长PM到S,使MS=NF,连接OS,则∠EOF与∠EOS的数量关系为 ,线段NF、EM、EF的数量关系为
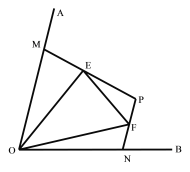
⑵如图2,点M、N分别在∠AOB的边OA、OB上,且OM=ON,![]() , E、F分别为线段MP、NP上的点,且∠EOF=
, E、F分别为线段MP、NP上的点,且∠EOF=![]() ∠AOB,⑴中的线段NF、EM、EF的数量关系是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明。
∠AOB,⑴中的线段NF、EM、EF的数量关系是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明。
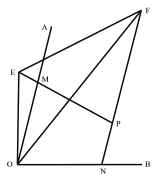
⑶如图3,点M、N分别在∠AOB的边OA、OB上,且OM=ON,![]() , E、F分别为线段PM、NP延长线上的点,且∠EOF=
, E、F分别为线段PM、NP延长线上的点,且∠EOF=![]() ∠AOB,⑴中的线段NF、EM、EF的数量关系是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明。
∠AOB,⑴中的线段NF、EM、EF的数量关系是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个正整数能表示成两个连续偶数的平方差,那么这个正整数为“神秘数”.
如:![]()
![]()
![]()
因此,4,12,20这三个数都是神秘数.
(1)28和2012这两个数是不是神秘数?为什么?
(2)设两个连续偶数为![]() 和
和![]() (其中
(其中![]() 为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
(3)两个连续奇数的平方差(取正数)是不是神秘数?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地雪灾发生之后,灾区急需帐篷。某车间的甲、乙两名工人分别同时生产同种帐篷上的同种零件,他们一天生产零件y(个)与生产时间t(时)的函数关系如图所示。
①甲、乙中______先完成一天的生产任务;在生产过程中,______因机器故障停止生产______小时。
②当t=______时,甲、乙生产的零件个数相等。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com