
����Ŀ��ijѧУΪ����ǿѧ�����ʣ�����������������������Ŀ��A����Bƹ����C������D����ӣ�Ϊ�˽�ѧ����ϲ����һ�ֻ��Ŀ�������ȡ�˲���ѧ�����е��飬�������������Ƴ���������������ͳ��ͼ����ش��������⣺ 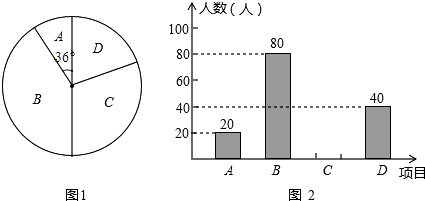
��1����α������ѧ�������ˣ�
��2�����㽫����ͳ��ͼ������ɣ�
��3����ƽʱ��ƹ������Ŀѵ���У��ס��ҡ����������˱������㣬�־�����������ͬѧ����ѡ�����μ�ƹ�����������ǡ��ѡ�мס�����λͬѧ�ĸ��ʣ�����״ͼ���б�����𣩣�
���𰸡�
��1��200
��2���⣺C��Ŀ��Ӧ����Ϊ��200��20��80��40=60���ˣ���
������ͼ��
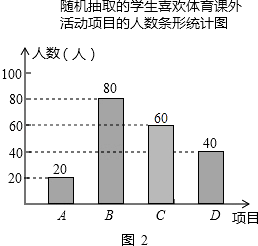
��3���⣺�б����£�
�� | �� | �� | �� | |
�� | �� | ���ң��ף� | �������ף� | �������ף� |
�� | ���ף��ң� | �� | �������ң� | �������ң� |
�� | ���ף����� | ���ң����� | �� | ���������� |
�� | ���ף����� | ���ң����� | ���������� | �� |
�߹���12�ֵȿ��ܵ������ǡ��ѡ�мס�����λͬѧ����2�֣�
��P��ѡ�мס��ң�= ![]() =
= ![]() ��
��
���������⣺��1����������ã���α������ѧ������20�� ![]() =200���ˣ��� �ʴ�Ϊ��200��
=200���ˣ��� �ʴ�Ϊ��200��
��1���������֪��α������ѧ������20�� ![]() =200���ˣ�����2���������C��Ŀ��Ӧ����Ϊ��200��20��80��40=60���ˣ����̶��ɲ�ȫ����ͳ��ͼ����3�����ȸ������⻭����״ͼ��Ȼ������״ͼ������еȿ��ܵĽ����ǡ��ѡ�мס�����λͬѧ������������ø��ʹ�ʽ������ô𰸣�
=200���ˣ�����2���������C��Ŀ��Ӧ����Ϊ��200��20��80��40=60���ˣ����̶��ɲ�ȫ����ͳ��ͼ����3�����ȸ������⻭����״ͼ��Ȼ������״ͼ������еȿ��ܵĽ����ǡ��ѡ�мס�����λͬѧ������������ø��ʹ�ʽ������ô𰸣�


 ��ĩ���䵥Ԫ�����ิϰ��ϵ�д�
��ĩ���䵥Ԫ�����ิϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ˮ��������������2014��12����ʽͨˮ���������߶������г������棬���ϡ��ӱ�������������ĸ�ʡ���У���ˮ��Դ����̬�Ƶõ����⣬��Ч�ٽ��˵���ˮ��Դ�ĺ����ͻָ�.��������ͬ����ȣ���������ˮ��ˮλ�½���Ϊ����������Ϊ������¼��2013�����������������ˮˮλ�ı仯�õ��±���
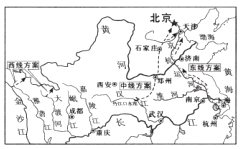
ʱ�� | 2013��� | 2014��� | 2015��� | 2016��� | 2017��� | 2018��9�µ� |
����ˮλ������ͬ�ȱ仯������λ�� | -0.25 | -1.14 | -0.09 | +0.52 | +0.26 | +2.12 |
���¹���2013��������������ˮˮλ��˵������ȷ���ǣ� ��
A. ��2014���ʼ����������ˮˮλ���½����Ƶõ�����
B. ��2015���2016��ף���������ˮˮλ�״λ���
C. 2013��������ÿ����ĵ���ˮλ������ͬ�ȵĻ�����������2018��
D. 2018��9�µĵ���ˮλ����2012��ĵ���ˮˮλ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
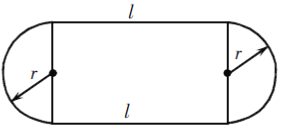
����Ŀ����ͼ���ٳ�������Ϊ��Բ�Σ��м���һ�������Σ� ��֪��Բ�İ뾶Ϊr��ֱ�ܵ��ij�Ϊl�����ù���r��l�Ķ���ʽ��ʾ����ٳ�������� �������ʽ�ֽܷ���ʽ�����ܣ�������ֽ���ʽ�������㵱r��40m��l��30��mʱ�ٳ������(���������)�������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
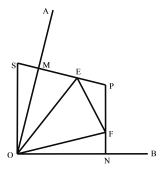
����Ŀ������ͼ1����M��N�ֱ��ڡ�AOB�ı�OA��OB�ϣ���OM��ON������M��N�ֱ���MP��OA��NP��OB��MP��NP����P��E��F�ֱ�Ϊ�߶�MP��NP�ϵĵ㣬�ҡ�EOF��![]() ��AOB���ӳ�PM��S��ʹMS��NF������OS�����EOF���EOS��������ϵΪ ���߶�NF��EM��EF��������ϵΪ
��AOB���ӳ�PM��S��ʹMS��NF������OS�����EOF���EOS��������ϵΪ ���߶�NF��EM��EF��������ϵΪ
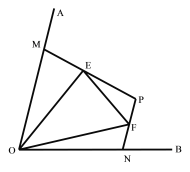
����ͼ2����M��N�ֱ��ڡ�AOB�ı�OA��OB�ϣ���OM��ON��![]() �� E��F�ֱ�Ϊ�߶�MP��NP�ϵĵ㣬�ҡ�EOF��
�� E��F�ֱ�Ϊ�߶�MP��NP�ϵĵ㣬�ҡ�EOF��![]() ��AOB�����е��߶�NF��EM��EF��������ϵ�Ƿ���Ȼ����������������֤����������������д������֮���������ϵ����֤����
��AOB�����е��߶�NF��EM��EF��������ϵ�Ƿ���Ȼ����������������֤����������������д������֮���������ϵ����֤����
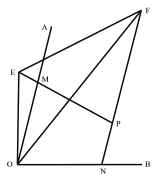
����ͼ3����M��N�ֱ��ڡ�AOB�ı�OA��OB�ϣ���OM��ON��![]() �� E��F�ֱ�Ϊ�߶�PM��NP�ӳ����ϵĵ㣬�ҡ�EOF��
�� E��F�ֱ�Ϊ�߶�PM��NP�ӳ����ϵĵ㣬�ҡ�EOF��![]() ��AOB�����е��߶�NF��EM��EF��������ϵ�Ƿ���Ȼ����������������֤����������������д������֮���������ϵ����֤����
��AOB�����е��߶�NF��EM��EF��������ϵ�Ƿ���Ȼ����������������֤����������������д������֮���������ϵ����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ϊ�ӿ�������彨�裬���������Ҹ����ݣ���A��B�����ׯ������ȫ��Ľ�������Ԥ�㣬����һ��A��������ׯ��һ��B��������ׯ�����ʽ�300��Ԫ����������2��A���ׯ��5��B���ׯ��Ͷ���ʽ�1140��Ԫ��
��1������һ��A��������ׯ��һ��B��������ׯ������ʽ�ֱ��Ƕ�����Ԫ��
��2������3��A��������ׯ��6��B���ׯ�Ľ������ʽ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����һ���������ܱ�ʾ����������ż����ƽ�����ô���������Ϊ����������.
�磺![]()
![]()
![]()
��ˣ�4��12��20������������������.
��1��28��2012���������Dz�����������Ϊʲô��
��2������������ż��Ϊ![]() ��
��![]() (����
(����![]() Ϊ�Ǹ�����)��������������ż���������������4�ı�������˵������.
Ϊ�Ǹ�����)��������������ż���������������4�ı�������˵������.
��3����������������ƽ���ȡ�������Dz�������������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������6������һ��������ϰ�У�����Ա����һ��25����������AB����ͼб����һ��ǽ�ϣ����ӵ�B��ǽ��C�ľ���Ϊ7����

��1����������ӵĶ��˾������߶�AC�Ƕ��٣�
��2���������Ա�ӵ������Ҫ�����ӵײ���ˮƽ���� ����ͣ��DE��λ���������ݳ��Ȳ����������BD��Ϊ8������ô���ݵĶ������»��˶����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ijУ�ˡ����꼶����ѧ����˯������������ȡ�˸�У�ˡ����꼶����ѧ�����е��飬��֪��ȡ�İ��꼶����꼶��ѧ��������ͬ�����ó������õ����ݻ�����ͼ��ͳ��ͼ����
˯������ֶ��������
��� | ˯��ʱ��x��Сʱ�� |
A | 4.5��x��5.5 |
B | 5.5��x��6.5 |
C | 6.5��x��7.5 |
D | 7.5��x��8.5 |
E | 8.5��x��9.5 |
����ͼ���ṩ����Ϣ���ش��������⣺
����ֱ��д��ͳ��ͼ��a��ֵ ![]()
����˯��ʱ������6.5СʱΪ����˯�߲��㣬��Ӹ�У�ˡ����꼶�������һ��ѧ�������鵽������λѧ��˯�����ز���Ŀ����Էֱ��ж��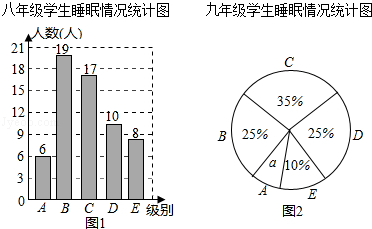
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧϰ�˶��θ�ʽ�������������Ƿ���һЩ���и��ŵ�ʽ�ӿ��Ա�ʾ����һ��ʽ�ӵ�ƽ�����磺
3+2![]() ��2+2
��2+2![]() +1��(
+1��(![]() )2+2
)2+2![]() +1��(
+1��(![]() +1)2��
+1)2��
5+2![]() ��2+2
��2+2![]() +3��(
+3��(![]() )2+2��
)2+2��![]() ��
��![]() +(
+(![]() )2��(
)2��(![]() +
+![]() )2
)2
(1)���������ʽ�ӵı仯���̣������и�ʽ������һ��ʽ�ӵ�ƽ������ʽ��
��4+2![]() ����6+4
����6+4![]()
(2)��a+4![]() ��(m+n
��(m+n![]() )2����a��m��n����������������a��ֵ��
)2����a��m��n����������������a��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com