练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果．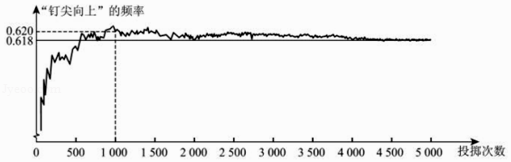
    下面有三个推断：
    ①当投掷次数是500时，计算机记录“钉尖向上”的次数是308，所以“钉尖向上”的概率是0.616；
    ②随着实验次数的增加，“钉尖向上”的频率总在0.618附近摆动，显示出一定的稳定性，可以估计“钉尖向上”的概率是0.618；
    ③若再次用计算机模拟实验，则当投掷次数为1000时，“钉尖向上”的概率一定是0.620．
    其中合理的是（ ）
    A.①
    B.②
    C.①②
    D.①③

    【答案】B
    【解析】解：当投掷次数是500时，计算机记录“钉尖向上”的次数是308，所以此时“钉尖向上”的可能性是：308÷500=0.616，但“钉尖向上”的概率不一定是0.616，故①错误， 随着实验次数的增加，“钉尖向上”的频率总在0.618附近摆动，显示出一定的稳定性，可以估计“钉尖向上”的概率是0.618．故②正确，
    若再次用计算机模拟实验，则当投掷次数为1000时，“钉尖向上”的概率可能是0.620，但不一定是0.620，故③错误，
    故选B．
    根据图形和各个小题的说法可以判断是否正确，从而可以解答本题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】甲、乙两地之间有一条笔直的公路，小明从甲地出发沿公路步行前往乙地，同时小亮从乙地出发沿公路骑车前往甲地，小亮到达甲地停留一段时间，原路原速返回，追上小明后两人一起步行到乙地.设小明与甲地的距离为(m)，小亮与甲地的距离为(m)，小明与小亮之间的距离为(m)，小明行走的时间为(min).，与之间的函数图象如图①，与之间的函数图象(部分)如图②.

    (1)求小亮从乙地到甲地过程中(m)与(min)之间的函数表达式;

    (2)求小亮从甲地返回到与小明相遇的过程中(m)与( min)之间的函数表达式;

    (3)在图②中，补全整个过程中(m)与(min)之间的函数图象，并确定的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】南水北调工程中线自2014年12月正式通水以来，沿线多座大中城市受益，河南、河北、北京及天津四个省（市）的水资源紧张态势得到缓解，有效促进了地下水资源的涵养和恢复.若与上年同期相比，北京地下水的水位下降记为负，回升记为正，记录从2013年底以来，北京地下水水位的变化得到下表：

    时间

    2013年底

    2014年底

    2015年底

    2016年底

    2017年底

    2018年9月底

    地下水位与上年同比变化量（单位：）

    -0.25

    -1.14

    -0.09

    +0.52

    +0.26

    +2.12

    以下关于2013年以来北京地下水水位的说法不正确的是（ ）

    A. 从2014年底开始，北京地下水水位的下降趋势得到缓解

    B. 从2015年底到2016年底，北京地下水水位首次回升

    C. 2013年以来，每年年底的地下水位与上年同比的回升量最大的是2018年

    D. 2018年9月底的地下水位低于2012年底的地下水水位

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知线段AB=2，MN⊥AB于点M，且AM=BM，P是射线MN上一动点，E，D分别是PA，PB的中点，过点A，M，D的圆与BP的另一交点C（点C在线段BD上），连结AC，DE．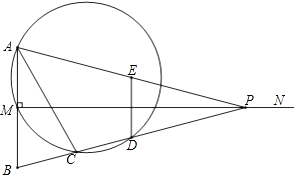

    （1）当∠APB=28°时，求∠B和 的度数；
    （2）求证：AC=AB．
    （3）在点P的运动过程中
    ①当MP=4时，取四边形ACDE一边的两端点和线段MP上一点Q，若以这三点为顶点的三角形是直角三角形，且Q为锐角顶点，求所有满足条件的MQ的值；
    ②记AP与圆的另一个交点为F，将点F绕点D旋转90°得到点G，当点G恰好落在MN上时，连结AG，CG，DG，EG，直接写出△ACG和△DEG的面积之比．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(本题10分) 如图1，将△ABC纸片沿中位线EH折叠，使点A的对称点D落在BC边上，再将纸片分别沿等腰△BED和等腰△DHC的底边上的高线EF,HG折叠,折叠后的三个三角形拼合形成一个矩形.类似地，对多边形进行折叠，若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩 形，这样的矩形称为叠合矩形.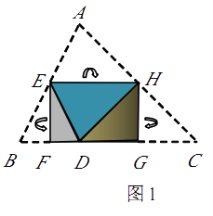


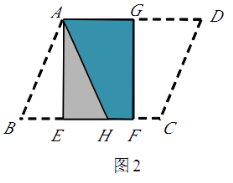
    （1）将□ABCD纸片按图2的方式折叠成一个叠合矩形AEFG，则操作形成的折痕分别是线段 ， ；S矩形AEFG:S□ABCD=
    （2）ABCD纸片还可以按图3的方式折叠成一个叠合矩形EFGH，若EF=5，EH=12，求AD的长.
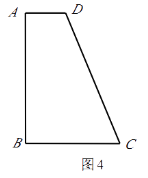
    （3）如图4，四边形ABCD纸片满足AD∥BC,AD<BC,AB⊥BC，AB=8,CD=10.小明把该纸片折叠，得到叠合正方形.请你帮助画出叠合正方形的示意图，并求出AD,BC的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

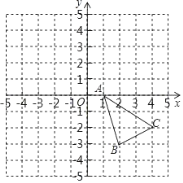
    【题目】如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（1，0），B（2，﹣3），C（4，﹣2）．

    （1）①画出△ABC关于x轴的对称图形△A1B1C1；②画出△A1B1C1向左平移3个单位长度后得到的△A2B2C2；

    （2）如果AC上有一点P（m，n）经过上述两次变换，那么对应A2C2上的点P2的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

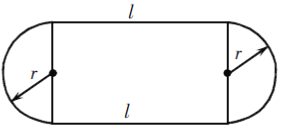
    【题目】如图，操场的两端为半圆形，中间是一个长方形． 已知半圆的半径为r，直跑道的长为l，请用关于r，l的多项式表示这个操场的面积． 这个多项式能分解因式吗？若能，请把它分解因式，并计算当r＝40m，l＝30πm时操场的面积(结果保留π)；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

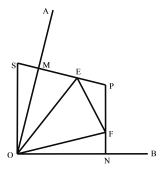
    【题目】⑴如图1，点M、N分别在∠AOB的边OA、OB上，且OM＝ON，过点M、N分别作MP⊥OA、NP⊥OB，MP、NP交于P，E、F分别为线段MP、NP上的点，且∠EOF＝∠AOB，延长PM到S，使MS＝NF，连接OS，则∠EOF与∠EOS的数量关系为 ，线段NF、EM、EF的数量关系为

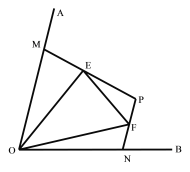
    ⑵如图2，点M、N分别在∠AOB的边OA、OB上，且OM＝ON，， E、F分别为线段MP、NP上的点，且∠EOF＝∠AOB，⑴中的线段NF、EM、EF的数量关系是否仍然成立？若成立，请证明；若不成立，请写出它们之间的数量关系，并证明。

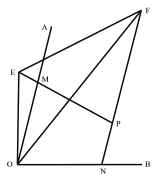
    ⑶如图3，点M、N分别在∠AOB的边OA、OB上，且OM＝ON，， E、F分别为线段PM、NP延长线上的点，且∠EOF＝∠AOB，⑴中的线段NF、EM、EF的数量关系是否仍然成立？若成立，请证明；若不成立，请写出它们之间的数量关系，并证明。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了解某校八、九年级部分学生的睡眠情况，随机抽取了该校八、九年级部分学生进行调查，已知抽取的八年级与九年级的学生人数相同，利用抽样所得的数据绘制如图的统计图表：
    睡眠情况分段情况如下

    组别

    睡眠时间x（小时）

    A

    4.5≤x＜5.5

    B

    5.5≤x＜6.5

    C

    6.5≤x＜7.5

    D

    7.5≤x＜8.5

    E

    8.5≤x＜9.5

    根据图表提供的信息，回答下列问题：
    （Ⅰ）直接写出统计图中a的值
    （Ⅱ）睡眠时间少于6.5小时为严重睡眠不足，则从该校八、九年级各随机抽一名学生，被抽到的这两位学生睡眠严重不足的可能性分别有多大？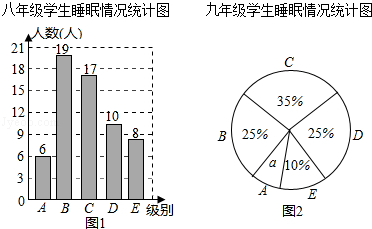

    查看答案和解析>>

    同步练习册答案