
����Ŀ���ס�������֮����һ����ֱ�Ĺ�·![]() ��С���Ӽس����ع�·
��С���Ӽس����ع�·![]() ����ǰ���ҵأ�ͬʱС�����ҵس����ع�·
����ǰ���ҵأ�ͬʱС�����ҵس����ع�·![]() �ﳵǰ���أ�С�������ͣ��һ��ʱ�䣬ԭ·ԭ�ٷ��أ���С��������һ���е��ҵ�.��С����صľ���Ϊ
�ﳵǰ���أ�С�������ͣ��һ��ʱ�䣬ԭ·ԭ�ٷ��أ���С��������һ���е��ҵ�.��С����صľ���Ϊ![]() (m)��С����صľ���Ϊ
(m)��С����صľ���Ϊ![]() (m)��С����С��֮��ľ���Ϊ
(m)��С����С��֮��ľ���Ϊ![]() (m)��С�����ߵ�ʱ��Ϊ
(m)��С�����ߵ�ʱ��Ϊ![]() (min).
(min).![]() ��
��![]() ��
��![]() ֮��ĺ���ͼ����ͼ�٣�
֮��ĺ���ͼ����ͼ�٣�![]() ��
��![]() ֮��ĺ���ͼ��(����)��ͼ��.
֮��ĺ���ͼ��(����)��ͼ��.
(1)��С�����ҵص��ع�����![]() (m)��
(m)��![]() (min)֮��ĺ�������ʽ;
(min)֮��ĺ�������ʽ;
(2)��С���Ӽط��ص���С�������Ĺ�����![]() (m)��
(m)��![]() ( min)֮��ĺ�������ʽ;
( min)֮��ĺ�������ʽ;
(3)��ͼ���У���ȫ����������![]() (m)��
(m)��![]() (min)֮��ĺ���ͼ��ȷ��
(min)֮��ĺ���ͼ��ȷ��![]() ��ֵ.
��ֵ.

���𰸡�(1) ![]() ��(2)
��(2) ![]() ��(3)
��(3)![]() ����ȫͼ�������.
����ȫͼ�������.
��������
(1)��С�����ҵص��ع�����y1���ף���x�����ӣ�֮��ĺ�����ϵʽΪy1=k1x+b���ɴ���ϵ��������ͼ��Ϳ����������ʽ��
(2)�ȸ��ݺ���ͼ��������ҵ��ٶȣ�Ȼ����������Ϳ������С����С����ʱ�䣬�Ϳ������С���Ӽط��ص���С�������Ĺ�����s���ף���x�����ӣ�֮��ĺ�����ϵʽ��
(3)�ȸ����������⽨�����̾Ϳ������aֵ��10���Ӽס����ߵ�·�̾������ľ��룬14����С���ߵ�·�̺�С����С��ʱ��ʱ��Ϳ��Բ�����ͼ��.
(1)��С�����ҵص��ع�����y1���ף���x�����ӣ�֮��ĺ�����ϵʽΪy1=k1x+b����ͼ�ã�![]() ����ã�
����ã�![]() ��
��
��y1=��240x+2400��
(2)�����⣬��С�����ٶ�Ϊ��2400��40=60��/�֣�С�����ٶ�Ϊ��2400��10=240��/�֣�
��С���Ӽ���С����ʱ��Ϊ24��60�£�240��60��=8���ӣ�
��24����ʱ���˵ľ���Ϊ��s=24��60=1440��32����ʱS=0��
��s��x֮��ĺ�����ϵʽΪ��s=kx+b1�������⣬��![]() ��
��
��ã�![]() ��
��
��s=��180x+5760��
(3)�����⣬��a=2400�£�240+60��=8���ӣ�
��x=24ʱ��s=1440����x=32ʱ��S=0��
�������Ӧ�ĵ�Ϳ��Բ�ȫͼ����ͼ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��B��CΪ��O�ϵĵ㣬PC��O�㣬����O��D�㣬PD=OD����OB��AC��E�㣮 
��1���ж�A�Ƿ���PB���е㣬��˵�����ɣ�
��2������O�뾶Ϊ8������BC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A��B����֮���·��Ϊ2380�ף��ס������˷ֱ��A��B���س�����������У���֪���ȳ���5���Ӻ��Ҳų���������������A��B֮���C����������������������A�أ��Ҽ�����A��ǰ�У�����A��ʱֹͣ���ߣ��ҵ���A��ʱҲֹͣ���ߣ����������߹����У��ס������˾����ָ��Ե��ٶ��������ߣ��ס�����������·��y���ף���׳�����ʱ��x�����ӣ�֮��Ĺ�ϵ��ͼ��ʾ�����ҵ���A��ʱ������A������·�����ף� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y= ![]() x2��
x2�� ![]() x��
x�� ![]() ��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C���Գ�����x�ύ�ڵ�D����E��4��n�����������ϣ�
��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C���Գ�����x�ύ�ڵ�D����E��4��n�����������ϣ�
��1����ֱ��AE�Ľ���ʽ��
��2����PΪֱ��CE�·��������ϵ�һ�㣬����PC��PE������PCE��������ʱ������CD��CB����K���߶�CB���е㣬��M��CP�ϵ�һ�㣬��N��CD�ϵ�һ�㣬��KM+MN+NK����Сֵ��
��3����G���߶�CE���е㣬��������y= ![]() x2��
x2�� ![]() x��
x�� ![]() ��x��������ƽ�Ƶõ���������y�䣬y�侭����D��y��Ķ���Ϊ��F������������y��ĶԳ����ϣ��Ƿ����һ��Q��ʹ�á�FGQΪ���������Σ������ڣ�ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
��x��������ƽ�Ƶõ���������y�䣬y�侭����D��y��Ķ���Ϊ��F������������y��ĶԳ����ϣ��Ƿ����һ��Q��ʹ�á�FGQΪ���������Σ������ڣ�ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��ʾ�������н���ƽ��ֱ������ϵ��![]() �������������ֱ�Ϊ
�������������ֱ�Ϊ![]() ��
��![]() ��
��![]() .
.
(1)����![]() ����
����![]() ��ĶԳ�ͼ��
��ĶԳ�ͼ��![]() ��
��
(2)����ͼ�е�������ֻ��ֱ��(�����̶�)�������Ҫ��:(��������:������˱�ע��ĸ)
����ͼ����һ��![]() ��ʹ��
��ʹ��![]() ����
����![]() �ľ�����ȣ���
�ľ�����ȣ���![]() ;
;
����![]() ������һ��
������һ��![]() ��ʹ��
��ʹ��![]() ���ܳ���С���������ʱ��
���ܳ���С���������ʱ��![]() ������.
������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ͼ��(����OEFPMN)������ij�����ڸ��ٹ�·����ʻ�������ٶ���ʱ��ĺ�����ϵ������˵���У��������( )

A. ��5 minʱ�������ٶ���80 km/h
B. �ӵ�3 min����6 min��������ʻ��4 km
C. �� 6 min��9 min��������ʻ��6 km
D. �ӵ�9 min����12 min������һֱ�ڼ���ֱ���ٶȼ�Ϊ0 km/h
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������![]() �Ķ���
�Ķ���![]() ������ԭ�㣬����
������ԭ�㣬����![]() �ֱ���
�ֱ���![]() �ᣬ
�ᣬ![]() ����������ϣ�
����������ϣ�![]() ��
��![]() ��
Ϊ��![]() ���е㣬
���е㣬![]() �DZ�
�DZ�![]() �ϵ�һ�����㣬��
�ϵ�һ�����㣬��![]() ���ܳ���Сʱ����
���ܳ���Сʱ����![]() ������Ϊ_________.
������Ϊ_________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABCD�������Գ���Ϊ�����ᣬ��A������Ϊ��2,1��.һ����ֽ�ϻ���һ�����һ�������ߣ�ƽ����ֽ����������A�غϣ���ʱ�����ߵĺ�������ʽΪy=x2 �� �ٴ�ƽ����ֽ��ʹ��������C�غϣ���������ߵĺ�������ʽ��Ϊ�� ��
A.y=x2+8x+14
B.y=x2-8x+14
C.y=x2+4x+3
D.y=x2-4x+3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ü����ģ�����Ͷ��һöͼ����ij��ʵ��Ľ���� 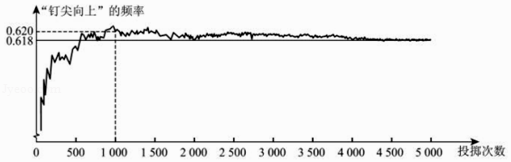
�����������ƶϣ�
�ٵ�Ͷ��������500ʱ���������¼���������ϡ��Ĵ�����308�����ԡ��������ϡ��ĸ�����0.616��
������ʵ����������ӣ����������ϡ���Ƶ������0.618�����ڶ�����ʾ��һ�����ȶ��ԣ����Թ��ơ��������ϡ��ĸ�����0.618��
�����ٴ��ü����ģ��ʵ�飬��Ͷ������Ϊ1000ʱ�����������ϡ��ĸ���һ����0.620��
���к������ǣ� ��
A.��
B.��
C.�٢�
D.�٢�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com