
【题目】如图,A、B、C为⊙O上的点,PC过O点,交⊙O于D点,PD=OD,若OB⊥AC于E点. 
(1)判断A是否是PB的中点,并说明理由;
(2)若⊙O半径为8,试求BC的长.
【答案】
(1)解:A是PB的中点,
理由:连接AD,

∵CD是⊙O的直径,
∴AD⊥AC,
∵OB⊥AC,
∴AD∥OB,
∵PD=OD,
∴PA=AB,
∴A是PB的中点
(2)∵AD∥OB,
∴△APD∽△BPO,
∴ ![]() ,
,
∵⊙O半径为8,
∴OB=8,
∴AD=4,
∴AC= ![]() =4
=4 ![]() ,
,
∵OB⊥AC,
∴AE=CE=2 ![]() ,
,
∵OE= ![]() AD=2,
AD=2,
∴BE=6,
∴BC= ![]() =4
=4 ![]() .
.
【解析】(1)连接AD,由CD是⊙O的直径,得到AD⊥AC,推出AD∥OB,根据平行线等分线段定理得到PA=AB;(2)根据相似三角形的性质得到OB=8,求得AD=4,根据勾股定理得到AC= ![]() =4
=4 ![]() ,根据垂径定理得到AE=CE=2
,根据垂径定理得到AE=CE=2 ![]() ,由勾股定理即可得到结论
,由勾股定理即可得到结论
【考点精析】掌握勾股定理的概念和垂径定理是解答本题的根本,需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
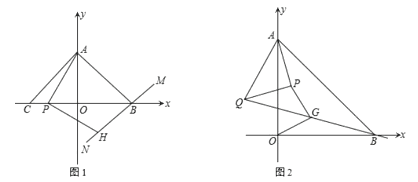
【题目】如图,在平面直角坐标系中,A(0,a)、B(b,0)、C(c,0),且![]() =0.
=0.
(1)直接写出 A、B、C 各点的坐标:A_______;B__________;C_____;
(2)过 B 作直线 MN⊥AB,P 为线段 OC 上的一动点,AP⊥PH 交直线 MN 于点 H,证明:PA=PH.
(3)在(1)的条件下,若在点 A 处有一个等腰 Rt△APQ 绕点 A 旋转,且 AP=PQ,∠APQ=90°,连接 BQ,点 G 为 BQ 的中点,试猜想线段 OG 与线段 PG 的数量关系与位置关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=(m+2)x2﹣2(m+2)x﹣m+5,其中m+2>0.
(1)求该二次函数的对称轴方程;
(2)过动点C(0,n)作直线l⊥y轴. ①当直线l与抛物线只有一个公共点时,求n与m的函数关系;
②若抛物线与x轴有两个交点,将抛物线在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象.当n=7时,直线l与新的图象恰好有三个公共点,求此时m的值;
(3)若对于每一个给定的x的值,它所对应的函数值都不小于1,求m的取值范围. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从2开始,连续的偶数相加,它们和的情况如表:
加数的个数n | S |
1 | 2=1×2 |
2 | 2+4=6=2×3 |
3 | 2+4+6=15=3×4 |
4 | 2+4+6+8=20=4×5 |
5 | 2+4+6+8+10=30=5×6 |
(1)根据表中的规律猜想:用n的式子表示S的公式为:S=2+4+6+8+…+2n=;
(2)如下数表是由从1开始的连续自然数组成,观察规律:
①第n行的第一个数可用含n的式子表示为;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是某新建厂区示意图,∠A=75°,∠B=45°,BC⊥CD,AB=500 ![]() 米,AD=200米,现在要在厂区四周建围墙,求围墙的长度有多少米?
米,AD=200米,现在要在厂区四周建围墙,求围墙的长度有多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,DC∥AB,BD平分∠ABC,CD=4.
(1)求BC的长;
(2)如图2,若∠ABC=60°,过点D作DE⊥AB,过点C作CF⊥BD,垂足分别为E、F,连接EF.请判断△DEF的形状并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一张对边互相平行的纸条,折成如图所示,EF是折痕,若∠EFB=32°,则下列结论正确的有( )

(1)∠C′EF=32°;(2)∠AEC=148°;(3)∠BGE=64°;(4)∠BFD=116°.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=AC,∠C=70°,△AB′C′与△ABC 关于直线 EF对称,∠CAF=10°,连接 BB′,则∠ABB′的度数是( )

A. 30° B. 35° C. 40° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地之间有一条笔直的公路![]() ,小明从甲地出发沿公路
,小明从甲地出发沿公路![]() 步行前往乙地,同时小亮从乙地出发沿公路
步行前往乙地,同时小亮从乙地出发沿公路![]() 骑车前往甲地,小亮到达甲地停留一段时间,原路原速返回,追上小明后两人一起步行到乙地.设小明与甲地的距离为
骑车前往甲地,小亮到达甲地停留一段时间,原路原速返回,追上小明后两人一起步行到乙地.设小明与甲地的距离为![]() (m),小亮与甲地的距离为
(m),小亮与甲地的距离为![]() (m),小明与小亮之间的距离为
(m),小明与小亮之间的距离为![]() (m),小明行走的时间为
(m),小明行走的时间为![]() (min).
(min).![]() ,
,![]() 与
与![]() 之间的函数图象如图①,
之间的函数图象如图①,![]() 与
与![]() 之间的函数图象(部分)如图②.
之间的函数图象(部分)如图②.
(1)求小亮从乙地到甲地过程中![]() (m)与
(m)与![]() (min)之间的函数表达式;
(min)之间的函数表达式;
(2)求小亮从甲地返回到与小明相遇的过程中![]() (m)与
(m)与![]() ( min)之间的函数表达式;
( min)之间的函数表达式;
(3)在图②中,补全整个过程中![]() (m)与
(m)与![]() (min)之间的函数图象,并确定
(min)之间的函数图象,并确定![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com