
【题目】从2开始,连续的偶数相加,它们和的情况如表:
加数的个数n | S |
1 | 2=1×2 |
2 | 2+4=6=2×3 |
3 | 2+4+6=15=3×4 |
4 | 2+4+6+8=20=4×5 |
5 | 2+4+6+8+10=30=5×6 |
(1)根据表中的规律猜想:用n的式子表示S的公式为:S=2+4+6+8+…+2n=;
(2)如下数表是由从1开始的连续自然数组成,观察规律:
①第n行的第一个数可用含n的式子表示为;
【答案】
(1)n(n+1)
(2)∵第一行的第一个数字1=12﹣0,
第二行的第一个数字3=22﹣1,
第三行的第一个数字7=32﹣2,
第四行的第一个数字13=42﹣3,
以此类推,第n行的第一个数字为n2﹣(n﹣1)=n2﹣n+1,
故答案为:n2﹣n+1;
②如果某行的第一个数为157,求其所在的行数.
以此类推,第n行的第一个数字为n2﹣(n﹣1)=n2﹣n+1,
故答案为:n2﹣n+1;
【解析】解:(1)2+4+6+8+…+2n=n ![]() =n(n+1).
=n(n+1).
所以答案是:n(n+1).
【考点精析】认真审题,首先需要了解数与式的规律(先从图形上寻找规律,然后验证规律,应用规律,即数形结合寻找规律).


科目:初中数学 来源: 题型:
【题目】某环保小组为了了解世博园的游客在园区内购买瓶装饮料数量的情况,一天,他们分别在A,B,C三个出口处对离开园区的游客进行调查,并将在A出口调查所得到的数据整理后绘成了如图所示的统计图:

(1)在A出口的被调查游客中,购买2瓶及2瓶以上饮料的游客人数占A出口的被调查游客人数的______%;
(2)试问:A出口的被调查游客在园区内人均购买了多少瓶饮料?
(3)已知B,C两个出口的被调查游客在园区内人均购买饮料的数量如下表所示:
出口 | B | C |
人均购买饮料数量(瓶) | 3 | 2 |
若C出口的被调查人数比B出口的被调查人数多2万人,且B,C两个出口的被调查游客在园区内共购买了49万瓶饮料,试问:B出口的被调查游客有多少万人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,P是BC上一点,E是AB上一点,PD平分∠APC,PE⊥PD,连接DE交AP于F,在以下判断中,不正确的是( )
A.当P为BC中点,△APD是等边三角形
B.当△ADE∽△BPE时,P为BC中点
C.当AE=2BE时,AP⊥DE
D.当△APD是等边三角形时,BE+CD=DE
查看答案和解析>>
科目:初中数学 来源: 题型:
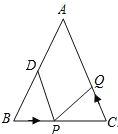
【题目】如图,在等腰![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
(1)如果点![]() 在底边
在底边![]() 上且以
上且以![]() 的速度由
的速度由![]() 点向
点向![]() 点运动,同时点
点运动,同时点![]() 在腰
在腰![]() 上由
上由![]() 向
向![]() 点运动.
点运动.
①如果点![]() 与点
与点![]() 的运动速度相等,求经过多少秒后
的运动速度相等,求经过多少秒后![]() ;
;
②如果点![]() 与点
与点![]() 的运动速度不相等,当点
的运动速度不相等,当点![]() 的运动速度为多少时,能够使
的运动速度为多少时,能够使![]() 与
与![]() 全等?
全等?
(2)若点![]() 以②中的运动速度从点
以②中的运动速度从点![]() 出发,点
出发,点![]() 以
以![]() 速度从点
速度从点![]() 同时出发,都逆时针沿
同时出发,都逆时针沿![]() 三边运动,直接写出当点
三边运动,直接写出当点![]() 与点
与点![]() 第一次相遇时
第一次相遇时![]() 的运动的路程.
的运动的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C为⊙O上的点,PC过O点,交⊙O于D点,PD=OD,若OB⊥AC于E点. 
(1)判断A是否是PB的中点,并说明理由;
(2)若⊙O半径为8,试求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1为放置在水平桌面上的某创意可折叠台灯的平面示意图,将其抽象成图2,量的∠DCB=60°,∠CDE=150°,灯杆CD的长为40cm,灯管DE的长为26cm,底座AB的厚度为2cm,不考虑其他因素,分别求出DE与水平卓,面(AB所在的直线)所成的夹角度数和台灯的高(点E到桌面的距离).(结果保留根号) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y= ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.
(1)求直线AE的解析式;
(2)点P为直线CE下方抛物线上的一点,连接PC,PE.当△PCE的面积最大时,连接CD,CB,点K是线段CB的中点,点M是CP上的一点,点N是CD上的一点,求KM+MN+NK的最小值;
(3)点G是线段CE的中点,将抛物线y= ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() 沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com