练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

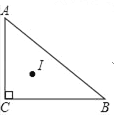
    【题目】如图，Rt△ABC中，∠C=90°，AB=5，BC=4，AC=3，点I为Rt△ABC三条角平分线的交点，则点I到边AB的距离为_____．

    【答案】1

    【解析】

    根据角平分线的性质得到IE=IF=ID，设IE=x，然后利用三角形面积公式得到S△ABC=S△IAB+S△IAC+S△ICB，于是可得到关于x的方程，从而可得到IF的长度．

    解：∵在△ABC中，∠C=90°，BC=4，CA=3，AB=5，

    ∵点I为△ABC的三条角平分线的交点，
    ∴IE=IF=ID，
    设IE=x，
    ∵S△ABC=S△IAB+S△IAC+S△ICB，
    ∴×4×3=IF×5+IE×3+ID×4，
    ∴5x+3x+4x=12，
    ∴x=1，
    ∴点I到AB的距离等于1．
    故答案为：1

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】三角板是学习数学的重要工具，将一副三角板中的两块直角三角板的直角顶点按如图方式叠放在一起，当且点在直线的上方时，解决下列问题：（友情提示：，，．

    （1）①若，则的度数为　　；

    ②若，则的度数为　　；

    （2）由（1）猜想与的数量关系，并说明理由．

    （3）这两块三角板是否存在一组边互相平行？若存在，请直接写出的角度所有可能的值（不必说明理由）；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】近年来由于空气质量的变化，以及人们对自身健康的关注程度不断提高，空气净化器成为很多家庭的新电器．某品牌的空气净化器厂家为进一步了解市场，制定生产计划，根据2016年下半年销售情况绘制了如下统计图，其中同比增长率=（ ﹣1）×100%，下面有四个推断：

    ①2016年下半年各月销售量均比2015年同月销售量增多
    ②第四季度销售量占下半年销售量的七成以上
    ③下半年月均销售量约为16万台
    ④下半年月销售量的中位数不超过10万台
    其中合理的是（ ）
    A.①②
    B.①④
    C.②③
    D.③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某公司招聘一名部门经理，对A、B、C三位候选人进行了三项测试，包括语言表达、微机操作、商品知识，各项成绩的权重分别是3，3，4，三人的成绩如下表：

    候选人

    语言表达

    微机操作

    商品知识

    A

    60

    80

    70

    B

    50

    70

    80

    C

    60

    80

    65

    请你通过计算分析一下谁会被录取？若想要B被录取，如何设计各种成绩的权重？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法中，正确的是( )

    A. 平面内，没有公共点的两条线段平行

    B. 平面内，没有公共点的两条射线平行

    C. 没有公共点的两条直线互相平行

    D. 互相平行的两条直线没有公共点

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知 A（﹣2，3）、B（﹣6，0）、C（﹣1，0）．

    (1)请在图中作出△ABC 关于 y 轴对称的△，并求出△的面积；

    (2)写出 、 的坐标 __________；__________；

    (3)若△DBC 与△ABC 全等，则 D 的坐标为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

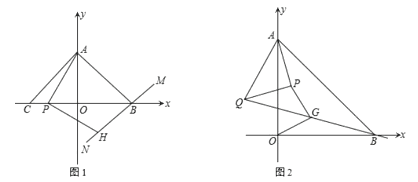
    【题目】如图，在平面直角坐标系中，A（0，a）、B（b，0）、C（c，0），且＝0．

    (1)直接写出 A、B、C 各点的坐标：A_______；B__________；C_____；

    (2)过 B 作直线 MN⊥AB，P 为线段 OC 上的一动点，AP⊥PH 交直线 MN 于点 H，证明：PA＝PH．

    (3)在（1）的条件下，若在点 A 处有一个等腰 Rt△APQ 绕点 A 旋转，且 AP＝PQ，∠APQ＝90°，连接 BQ，点 G 为 BQ 的中点，试猜想线段 OG 与线段 PG 的数量关系与位置关系，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，直线y=kx+b（k≠0）与双曲线y= 相交于点A（m，3），B（﹣6，n），与x轴交于点C．
    （1）求直线y=kx+b（k≠0）的解析式；
    （2）若点P在x轴上，且S△ACP= S△BOC ， 求点P的坐标（直接写出结果）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】从2开始，连续的偶数相加，它们和的情况如表：

    加数的个数n

    S

    1

    2=1×2

    2

    2+4=6=2×3

    3

    2+4+6=15=3×4

    4

    2+4+6+8=20=4×5

    5

    2+4+6+8+10=30=5×6


    （1）根据表中的规律猜想：用n的式子表示S的公式为：S=2+4+6+8+…+2n=；
    （2）如下数表是由从1开始的连续自然数组成，观察规律：

    ①第n行的第一个数可用含n的式子表示为；

    查看答案和解析>>

    同步练习册答案