
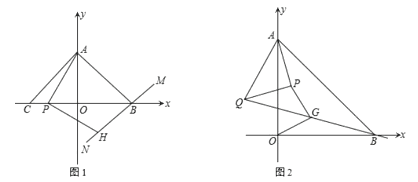
【题目】如图,在平面直角坐标系中,A(0,a)、B(b,0)、C(c,0),且![]() =0.
=0.
(1)直接写出 A、B、C 各点的坐标:A_______;B__________;C_____;
(2)过 B 作直线 MN⊥AB,P 为线段 OC 上的一动点,AP⊥PH 交直线 MN 于点 H,证明:PA=PH.
(3)在(1)的条件下,若在点 A 处有一个等腰 Rt△APQ 绕点 A 旋转,且 AP=PQ,∠APQ=90°,连接 BQ,点 G 为 BQ 的中点,试猜想线段 OG 与线段 PG 的数量关系与位置关系,并证明你的结论.
【答案】(1)( 0,3),(3,0),(﹣3,0);(2)见解析;(3)见解析.
【解析】
(1)根据非负数的性质得到a=3,b=3,C=-3,于是得到结论;
(2)利用A(0,3)、B(3,0) ,C(-3,0),得到ΔABC,ΔOAC,ΔOAB都是等腰直角三角形,如图1,过点P作PG//AB交y轴与G,则∠4=∠6=45![]() ,再证明ΔAPG≌ΔPHB,得到PA=PH.
,再证明ΔAPG≌ΔPHB,得到PA=PH.
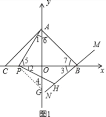
(3)OG=PG,OG⊥PG,理由:如图2,延长PG到R,使GR=PG,连接PO,OR,BR,证明
ΔPQG≌ΔBRG,得到PQ=BR,∠5=∠GBR,进而AP⊥PQ,再延长AP交BR于S,交OB于T,则AP⊥BR,证明ΔPAO≌ΔRBO得到PO=OR,∠1=∠2,所以ΔPOR为等腰直角三角形,根据PG=GR,所以OG⊥PG,OG=PG.
解:(1)∵![]() =0,
=0,
又∵![]() ≥0,|b﹣3|≥0,(c+3)2≥0,
≥0,|b﹣3|≥0,(c+3)2≥0,
∴a=b=3,c=﹣3,
∴A(0,3),B(3,0),C(﹣3,0),故答案为(0,3),(3,0),(﹣3,0).
(2)∵A(0,3)、B(3,0)、C(﹣3,0).
∴OA=OB=OC,
∴△ABC,△OAC,△OAB 都是等腰直角三角形,
∴∠6=∠7=45°,
如图 1,过点 P 作 PG∥AB 交 y 轴与 G,则∠4=∠6=45°,
∴OP=OG,
∴AO+OG=OB+OP,
即 AG=PB,
∵AP⊥PH,
∴∠2+∠5=90°,
∵∠1+∠5=90°,
∴∠1=∠2,
∵MN⊥AB,
∴∠3+∠7=90°,
∴∠3=45°,
∴∠3=∠4,
在△APG 和△PHB 中,
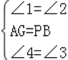
∴△APG≌△PHB(ASA),
∴PA=PH .
(3)结论:OG=PG,OG⊥PG,
理由:如图 2,延长 PG 到 R,使 GR=PG,连接 PO,OR,BR,
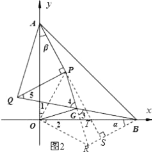
在△PQG 和△BRG 中,
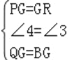
∴△PQG≌△BRG(SAS),
∴PQ=BR,∠5=∠GBR,
∴PQ∥BR,
∵AP⊥PQ,
延长 AP 交 BR 于 S,交 OB 于 T,则 AP⊥BR,
∵∠AOB=∠ASB=90°,∠ATR=∠BTS,
∴∠α=∠β,
∵PA=PQ,PQ=BR,
∴PA=BR,
在△PAO 和△RBO 中,
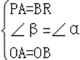
∴△PAO≌△RBO(SAS),
∴PO=OR ,∠1=∠2,
∵∠1+∠POB=90°,
∴∠POB+∠2=90°,
∴△POR 为等腰直角三角形,
∵PG=GR,
∴OG⊥PG,OG=PG.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=11,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点E,则DF的长为( )
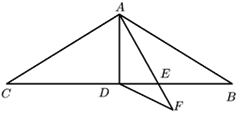
A. 4.5 B. 5 C. 5.5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名射击运动员中进行射击比赛,两人在相同条件下各射击10次,射击的成绩如图所示.

根据图中信息,回答下列问题:
(1)甲的平均数是___________,乙的中位数是______________;
(2)分别计算甲、乙成绩的方差,并从计算结果来分析,你认为哪位运动员的射击成绩更稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校组织340名师生进行长途考察活动,带有行李170件,计划租用甲、乙两种型号的汽车共10辆.经了解,甲车每辆最多能载40人和16件行李,乙车每辆最多能载30人和20件行李.
(1)请你帮助学校设计所有可行的租车方案.
(2)如果甲车的租金为每辆2 000元,乙车的租金为每辆1 800元,问哪种可行方案使租车费用最省?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是某娱乐节目中一个游戏环节的录制现场,场地由等边△ADE和正方形ABCD组成,正方形ABCD两条对角线交于点O,在AD的中点P处放置了一台主摄像机.游戏参与者行进的时间为x,与主摄像机的距离为y,若游戏参与者匀速行进,且表示y与x的函数关系式大致如图2所示,则游戏参与者的行进路线可能是( )
A.A→O→D
B.E→A→C
C.A→E→D
D.E→A→B
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上A,B两点对应的有理数分别为xA=﹣5和xB=6,动点P从点A出发,以每秒1个单位的速度沿数轴在A,B之间往返运动,同时动点Q从点B出发,以每秒2个单位的速度沿数轴在B,A之间往返运动.设运动时间为t秒.
(1)当t=2时,点P对应的有理数xP=______,PQ=______;
(2)当0<t≤11时,若原点O恰好是线段PQ的中点,求t的值;
(3)我们把数轴上的整数对应的点称为“整点”,当P,Q两点第一次在整点处重合时,直接写出此整点对应的数.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某环保小组为了了解世博园的游客在园区内购买瓶装饮料数量的情况,一天,他们分别在A,B,C三个出口处对离开园区的游客进行调查,并将在A出口调查所得到的数据整理后绘成了如图所示的统计图:

(1)在A出口的被调查游客中,购买2瓶及2瓶以上饮料的游客人数占A出口的被调查游客人数的______%;
(2)试问:A出口的被调查游客在园区内人均购买了多少瓶饮料?
(3)已知B,C两个出口的被调查游客在园区内人均购买饮料的数量如下表所示:
出口 | B | C |
人均购买饮料数量(瓶) | 3 | 2 |
若C出口的被调查人数比B出口的被调查人数多2万人,且B,C两个出口的被调查游客在园区内共购买了49万瓶饮料,试问:B出口的被调查游客有多少万人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C为⊙O上的点,PC过O点,交⊙O于D点,PD=OD,若OB⊥AC于E点. 
(1)判断A是否是PB的中点,并说明理由;
(2)若⊙O半径为8,试求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com