
【题目】图1是某娱乐节目中一个游戏环节的录制现场,场地由等边△ADE和正方形ABCD组成,正方形ABCD两条对角线交于点O,在AD的中点P处放置了一台主摄像机.游戏参与者行进的时间为x,与主摄像机的距离为y,若游戏参与者匀速行进,且表示y与x的函数关系式大致如图2所示,则游戏参与者的行进路线可能是( )
A.A→O→D
B.E→A→C
C.A→E→D
D.E→A→B
【答案】A
【解析】解:由题意可得,
当经过的路线是A→O→D时,从A→O,y随x的增大先减小后增大且图象对称,从O→D,y随x的增大先减小后增大且函数图象对称,故选项A符号要求;
当经过的路线是E→A→C时,从E→A,y随x的增大先减小后增大,但后来增大的最大值小于刚开始的值,故选项B不符号要求;
当经过的路线是A→E→D时,从A→E,y随x的增大先减小后增大,但后来增大的最大值大于于刚开始的值,故选项C不符号要求;
当经过的路线是E→A→B时,从E→A,y随x的增大先减小后增大,但后来增大的最大值小于刚开始的值,故选项D不符号要求;
故选A.
根据各个选项中的路线进行分析,看哪条路线符号图2的函数图象即可解答本题.


科目:初中数学 来源: 题型:
【题目】某校八年级共有8个班,241名同学,历史老师为了了解新中考模式下该校八年级学生选修历史学科的意向,请小红,小亮,小军三位同学分别进行抽样调查.三位同学调查结果反馈如下:
小红、小亮和小军三人中,你认为哪位同学的调查结果较好地反映了该校八年级同学选修历史的意向,请说出理由,并由此估计全年级有意向选修历史的同学的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司招聘一名部门经理,对A、B、C三位候选人进行了三项测试,包括语言表达、微机操作、商品知识,各项成绩的权重分别是3,3,4,三人的成绩如下表:
候选人 | 语言表达 | 微机操作 | 商品知识 |
A | 60 | 80 | 70 |
B | 50 | 70 | 80 |
C | 60 | 80 | 65 |
请你通过计算分析一下谁会被录取?若想要B被录取,如何设计各种成绩的权重?
查看答案和解析>>
科目:初中数学 来源: 题型:
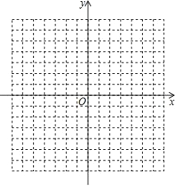
【题目】如图,已知 A(﹣2,3)、B(﹣6,0)、C(﹣1,0).
(1)请在图中作出△ABC 关于 y 轴对称的△![]() ,并求出△
,并求出△![]() 的面积;
的面积;
(2)写出 ![]() 、
、![]() 的坐标
的坐标 ![]() __________;
__________;![]() __________;
__________;
(3)若△DBC 与△ABC 全等,则 D 的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
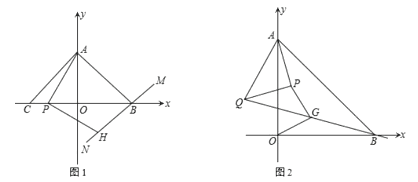
【题目】如图,在平面直角坐标系中,A(0,a)、B(b,0)、C(c,0),且![]() =0.
=0.
(1)直接写出 A、B、C 各点的坐标:A_______;B__________;C_____;
(2)过 B 作直线 MN⊥AB,P 为线段 OC 上的一动点,AP⊥PH 交直线 MN 于点 H,证明:PA=PH.
(3)在(1)的条件下,若在点 A 处有一个等腰 Rt△APQ 绕点 A 旋转,且 AP=PQ,∠APQ=90°,连接 BQ,点 G 为 BQ 的中点,试猜想线段 OG 与线段 PG 的数量关系与位置关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲沿周长为300米的环形跑道按逆时针方向跑步,速度为a米/秒,与此同时在甲后面100米的乙也沿该环形跑道按逆时针方向跑步,速度为3米/秒.
(1)若a=1,求甲、乙两人第一次相遇所用的时间;
(2)若a>3,甲、乙两人第一次相遇所用的时间为80秒,试求a的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线y= ![]() 相交于点A(m,3),B(﹣6,n),与x轴交于点C.
相交于点A(m,3),B(﹣6,n),与x轴交于点C. 
(1)求直线y=kx+b(k≠0)的解析式;
(2)若点P在x轴上,且S△ACP= ![]() S△BOC , 求点P的坐标(直接写出结果).
S△BOC , 求点P的坐标(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,DC∥AB,BD平分∠ABC,CD=4.
(1)求BC的长;
(2)如图2,若∠ABC=60°,过点D作DE⊥AB,过点C作CF⊥BD,垂足分别为E、F,连接EF.请判断△DEF的形状并证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com