
【题目】下列说法中,正确的是( )
A. 平面内,没有公共点的两条线段平行
B. 平面内,没有公共点的两条射线平行
C. 没有公共点的两条直线互相平行
D. 互相平行的两条直线没有公共点
科目:初中数学 来源: 题型:
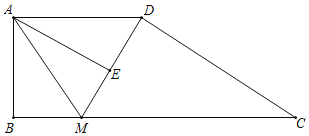
【题目】已知,梯形ABCD中,AD∥BC,∠ABC=90°,AB=3,BC=10,AD=5,M是BC边上的任意一点,联结DM,联结AM.
(1)若AM平分∠BMD,求BM的长;
(2)过点A作AE⊥DM,交DM所在直线于点E.
①设BM=x,AE=y求y关于x的函数关系式;
②联结BE,当△ABE是以AE为腰的等腰三角形时,请直接写出BM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥CD,且AB=CD.E、F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )
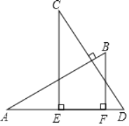
A. a+cB. b+cC. a﹣b+cD. a+b﹣c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列条件中,不能证明△ABD≌△ACD的是( )

A. AB=AC,BD=CD B. ∠B=∠C,BD=CD
C. ∠B=∠C,∠BAD=∠CAD D. ∠ADB=∠ADC,DB=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某职业高中机电班共有学生42人,其中男生人数比女生人数的2倍少3人.
(1)该班男生和女生各有多少人?
(2)某工厂决定到该班招录30名学生,经测试,该班男、女生每天能加工的零件数分别为50个和45个,为保证他们每天加工的零件总数不少于1460个,那么至少要招录多少名男学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景点的门票价格规定如表
购票人数 | 1﹣50人 | 51﹣100人 | 100人以上 |
每人门票价 | 12元 | 10元 | 8元 |
某校八年(1)(2)两班共102人去游览该景点,其中(1)班不足50人,(2)班多于50人,如果两班都以班为单位分别购票,则一共付款1118元
(1)两班各有多少名学生?
(2)如果你是学校负责人,你将如何购票?你的购票方法可节省多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空,完成下列说理过程
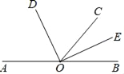
如图,已知点A,O,B在同一条直线上,OE平分∠BOC,∠DOE=90°
求证:OD是∠AOC的平分线;
证明:如图,因为OE是∠BOC的平分线,
所以∠BOE=∠COE.( )
因为∠DOE=90°
所以∠DOC+∠ =90°
且∠DOA+∠BOE=180°﹣∠DOE= °.
所以∠DOC+∠ =∠DOA+∠BOE.
所以∠ =∠ .
所以OD是∠AOC的平分线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com