
����Ŀ����գ��������˵������
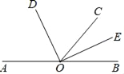
��ͼ����֪��A��O��B��ͬһ��ֱ���ϣ�OEƽ�֡�BOC����DOE��90��
��֤��OD�ǡ�AOC��ƽ���ߣ�
֤������ͼ����ΪOE�ǡ�BOC��ƽ���ߣ�
���ԡ�BOE����COE����������
����DOE��90��
���ԡ�DOC+�ϡ�����90��
�ҡ�DOA+��BOE��180�㩁��DOE�������㣮
���ԡ�DOC+�ϡ�������DOA+��BOE��
���ԡ��������ϡ�����
����OD�ǡ�AOC��ƽ���ߣ�
���𰸡���ƽ���߶��壻COE��90��COE��DOC��DOA��
��������
������֪�����۲�ͼ�Σ����ý�ƽ���ߵ����ʼ���֤��.
֤������ͼ����ΪOE�ǡ�BOC��ƽ���ߣ�
���ԡ�BOE����COE����ƽ���߶��壩
��Ϊ��DOE��90�㣬
���ԡ�DOC����COE��90�㣬
�ҡ�DOA����BOE��180�㩁��DOE��90�㣮
���ԡ�DOC����COE����DOA����BOE��
���ԡ�DOC����DOA��
����OD�ǡ�AOC��ƽ���ߣ�
�ʴ�Ϊ����ƽ���߶��壻COE��90��COE��DOC��DOA��


 ͬ������ϵ�д�
ͬ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���У���ȷ����( )
A. ƽ���ڣ�û�й�����������߶�ƽ��
B. ƽ���ڣ�û�й��������������ƽ��
C. û�й����������ֱ����ƽ��
D. ����ƽ�е�����ֱ��û�й�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P��˫����y= ![]() �ϣ���PΪԲ�ĵġ�P���������ᶼ���У�EΪy�Ḻ�����ϵ�һ�㣬PF��PE��x���ڵ�F����OF��OE��ֵ�ǣ� ��
�ϣ���PΪԲ�ĵġ�P���������ᶼ���У�EΪy�Ḻ�����ϵ�һ�㣬PF��PE��x���ڵ�F����OF��OE��ֵ�ǣ� �� 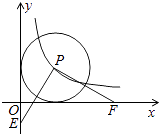
A.6
B.5
C.4
D.2 ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
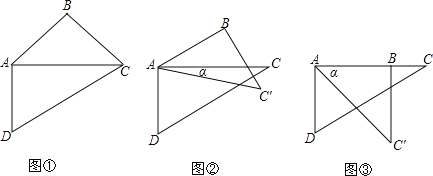
����Ŀ�������龳����ͼ�٣�����ABD����CAE�У�BD=AE����DBA=��EAC��AB=AC����֤����ABD�ա�CAE��������Ҫ֤����
����̽������ͼ�ڣ��ڵȱ���ABC�У���D��E�ֱ��ڱ�BC��AB�ϣ���BD=AE��AD��CE���ڵ�F����֤����ABD�ա�CAE��
����֤������ͼ�ۣ��ڵȱ���ABC�У���D��E�ֱ��ڱ�CB��BA���ӳ����ϣ���BD=AE����ABD����CAE�Ƿ�ȫ�ȣ����ȫ�ȣ���֤���������ȫ�ȣ���˵�����ɣ�
��չӦ�ã���ͼ�ܣ��ڵ����������У�AB=AC����O��AB�ߵĴ�ֱƽ������AC�Ľ��㣬��D��E�ֱ���OB��BA���ӳ����ϣ���BD=AE����BAC=50�㣬��AEC=32�������BAD�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�������������������,��������ȫ����Сѧ���С������������,ijѧУΪ����ѧ��������,���ٹ���һЩ���������.��֪��800Ԫ��������ĸ����ȹ�������ĸ�����2��,����ĵ���Ϊ���۵� ![]() .
.
��1������������ĵ��۷ֱ�Ϊ����Ԫ?
��2������ƻ��ò�����5200Ԫ������������60�� ,��ô����Ҫ������ٸ�����?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ǹ涨��![]() ��
��![]() ��a��0������a�ĸ�P���ݵ���a��p���ݵĵ���������
��a��0������a�ĸ�P���ݵ���a��p���ݵĵ���������![]() ��
��![]()
��1�����㣺![]() ��__��
��__��![]() ��__��
��__��
��2�����![]() ��
��![]() ����ôp��__�����
����ôp��__�����![]() ��
��![]() ����ôa��__��
����ôa��__��
��3�����![]() ��
��![]() ����a��pΪ������������������a��p��ȡֵ��
����a��pΪ������������������a��p��ȡֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ȡһ�����ǰ尴��ͼ��ʾƴ�ӣ��̶����ǰ�ADC�������ǰ�ABC�Ƶ�A˳ʱ�뷽����ת����ת�Ƕ�Ϊ����0�㣼����45�������õ���ABC�䣮
�ٵ���Ϊ���ٶ�ʱ��AB��DC��
�ڵ���ת��ͼ����ʾλ��ʱ����Ϊ���ٶȣ�
������BD����0�㣼����45��ʱ��̽���DBC��+��CAC��+��BDCֵ�Ĵ�С�仯��������������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����һԪһ�η��̵ĸ���һԪһ�β���ʽ��Ľ⣬��Ƹ�һԪһ�η���Ϊ�ò���ʽ��Ĺ������̣�
��1���ڷ��̢�3x��1=0���� ![]() ��x��(3x+1)=��5 �У�������
��x��(3x+1)=��5 �У�������![]() �Ĺ���������________
����������________
��2��������ʽ�� 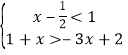 ��һ���������̵ĸ��������� ������������̿�����________��д��һ�����ɣ�
��һ���������̵ĸ��������� ������������̿�����________��д��һ�����ɣ�
��3�������� 3��x=2x��3+x= ![]() ���ǹ��� x �IJ���ʽ��
���ǹ��� x �IJ���ʽ�� ![]() �Ĺ������̣�ֱ��д�� m ��ȡֵ��Χ.
�Ĺ������̣�ֱ��д�� m ��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
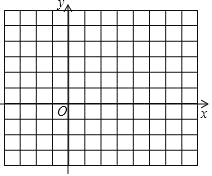
����Ŀ����ͼ����֪ABC �������������ֱ�Ϊ A(2, 3) ��B(6, 0) ��C(1, 0)
��1����ABC ��ֱ��д��ABC ����� ��
��2����A2 BC ��ABC �����ȣ������������ĵ� A2 �� �������ǵĺ�����Ϊ ��������Ϊ ��
��3����A3 BC ��ABC ȫ�ȣ���д������������ A3 �����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com