
【题目】问题情境:如图①,在△ABD与△CAE中,BD=AE,∠DBA=∠EAC,AB=AC,易证:△ABD≌△CAE.(不需要证明)
特例探究:如图②,在等边△ABC中,点D、E分别在边BC、AB上,且BD=AE,AD与CE交于点F.求证:△ABD≌△CAE.
归纳证明:如图③,在等边△ABC中,点D、E分别在边CB、BA的延长线上,且BD=AE.△ABD与△CAE是否全等?如果全等,请证明;如果不全等,请说明理由.
拓展应用:如图④,在等腰三角形中,AB=AC,点O是AB边的垂直平分线与AC的交点,点D、E分别在OB、BA的延长线上.若BD=AE,∠BAC=50°,∠AEC=32°,求∠BAD的度数.

【答案】证明见解析,∠BAD=18°
【解析】特例探究:利用等边三角形的三条边都相等、三个内角都是60°的性质推知AB=AC,∠DBA=∠EAC=60°,然后结合已知条件BD=AE,利用全等三角形的判定定理SAS证得△ABD≌△CAE.
归纳证明:△ABD与△CAE全等.利用等边三角形的三条边都相等、三个内角都是60°的性质以及三角形外角定理推知AB=AC,∠DBA=∠EAC=120°,然后结合已知条件BD=AE,利用全等三角形的判定定理SAS证得△ABD≌△CAE;
拓展应用:利用全等三角形(△ABD≌△CAE)的对应角∠BDA=∠AEC=32°,然后由三角形的外角定理求得∠BAD的度数.
解:特例探究:
证明:∵△ABC是等边三角形,
∴AB=AC,∠DBA=∠EAC=60°,
在△ABD与△CAE中, ,
,
∴△ABD≌△CAE(SAS);
归纳证明:
△ABD与△CAE全等.理由如下:
∵在等边△ABC中,AB=AC,∠ABC=∠BAC=60°,
∴∠DBA=∠EAC=120°.
在△ABD与△CAE中, ,
,
∴△ABD≌△CAE(SAS);
拓展应用:
∵点O在AB的垂直平分线上,
∴OA=OB,
∴∠OBA=∠BAC=50°,
∴∠EAC=∠DBC.
在△ABD与△CAE中, ,
,
∴△ABD≌△CAE(SAS),
∴∠BDA=∠AEC=32°,
∴∠BAD=∠OBA﹣∠BDA=18°.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
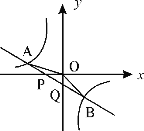
【题目】如图,已知直线 ![]() 与x轴、y轴相交于P、Q两点,与y=
与x轴、y轴相交于P、Q两点,与y=![]() 的图像相交于A(-2,m)、B(1,n)两点,连接OA、OB.给出下列结论: ①k1k2<0;②m+
的图像相交于A(-2,m)、B(1,n)两点,连接OA、OB.给出下列结论: ①k1k2<0;②m+![]() n=0; ③S△AOP= S△BOQ;④不等式k1x+b>
n=0; ③S△AOP= S△BOQ;④不等式k1x+b>![]() 的解集是x<-2或0<x<1,其中正确的结论的序号是 .
的解集是x<-2或0<x<1,其中正确的结论的序号是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车在匀速行驶过程中,路程s、速度v、时间t之间的关系为s=vt,下列说法正确的是( )
A. s、v、t都是变量B. s、t是变量,v是常量
C. v、t是变量,s是常量D. s、v是变量,t是常量
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣2,y1),B(1,y2)都在直线y=﹣2x+2上,则y1、y2的大小关系是( )
A. y1=y2B. y1<y2C. y1>y2D. y1≥y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“激情同在”第23届冬奥会于2018年2月在韩国平昌郡举行,场馆的建筑面积约是358 000平方米,将358 000用科学记数法表示为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明编了一个程序:输入任何一个有理数时,显示屏上的结果总等于输入的有理数的平方减去2得到的差。若他第一次输入-3,然后再将所得的结果输入,这时显示屏出现的结果是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京沈高速铁路赤峰至喀左段正在建设中,甲、乙两个工程队计划参与一项工程建设,甲队单独施工30天完成该项工程的![]() ,这时乙队加入,两队还需同时施工15天,才能完成该项工程.
,这时乙队加入,两队还需同时施工15天,才能完成该项工程.
(1)若乙队单独施工,需要多少天才能完成该项工程?
(2)若甲队参与该项工程施工的时间不超过36天,则乙队至少施工多少天才能完成该项工程?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com