
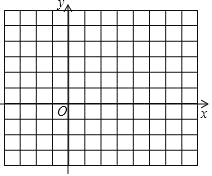
【题目】如图,已知ABC 三个顶点的坐标分别为 A(2, 3) 、B(6, 0) 、C(1, 0)
(1)画ABC ,直接写出ABC 的面积 ;
(2)若A2 BC 与ABC 面积相等,则满足条件的点 A2 有 个,它们的横坐标为 ,纵坐标为 ;
(3)若A3 BC 与ABC 全等,请写出满足条件的 A3 的坐标.
【答案】(1)图详见解析,![]() ;(2)无数个,任意实数,3 或3 ;(3)A3 的坐标(6, 3) 或(2, 3) 或(6, 3) .
;(2)无数个,任意实数,3 或3 ;(3)A3 的坐标(6, 3) 或(2, 3) 或(6, 3) .
【解析】
(1)画出△ABC,根据三角形的面积计算即可;
(2)若△A2BC与△ABC面积相等,则满足条件的点A2在直线l1和直线l2上,由此即可解决问题;
(3)若△A3BC与△ABC全等,满足条件的A3的坐标(6,3)或(-2,-3)或(6,-3);
(1)△ABC如图所示.![]()
故答案为![]() .
.
(2)若△A2BC与△ABC面积相等,则满足条件的点A2在直线l1和直线l2上,
∴则满足条件的点A2有无数个个,它们的横坐标为任意实数,纵坐标为3或3
故答案为无数个,任意实数,3或3;
(3)若△A3BC与△ABC全等,满足条件的A3的坐标(6,3)或(2,3)或(6,3);


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】填空,完成下列说理过程
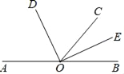
如图,已知点A,O,B在同一条直线上,OE平分∠BOC,∠DOE=90°
求证:OD是∠AOC的平分线;
证明:如图,因为OE是∠BOC的平分线,
所以∠BOE=∠COE.( )
因为∠DOE=90°
所以∠DOC+∠ =90°
且∠DOA+∠BOE=180°﹣∠DOE= °.
所以∠DOC+∠ =∠DOA+∠BOE.
所以∠ =∠ .
所以OD是∠AOC的平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,∠5=∠CDA=∠ABC,∠1=∠4,∠2=∠3,∠BAD+∠CDA=180°,填空:

∵∠5=∠CDA(已知),∴________∥________(内错角相等,两直线平行).
∵∠5=∠ABC(已知),∴________∥________(同位角相等,两直线平行).
∵∠2=∠3(已知),∴________∥________(内错角相等,两直线平行).
∵∠BAD+∠CDA=180°(已知),
∴________∥________(同旁内角互补,两直线平行).
∵∠5=∠CDA(已知),
又∠5与∠BCD互补,
∠CDA与________互补,
∴∠BCD=∠6(等角的补角相等),
∴________∥________(同位角相等,两直线平行).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)a3(-b3)2+(-2ab2)3;
(2)(a-b)10÷(b-a)3÷(b-a)3;
(3)-22+(-![]() )-2-(π-5)0-|-4|;
)-2-(π-5)0-|-4|;
(4)(x+y-3)(x-y+3);
(5)3x2y(2x-3y)-(2xy+3y2)(3x2-3y);
(6)(x-2y)(x+2y)-(x-2y)2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明对我校七年级(1)班喜欢什么球类运动的调查,下列图形中的左图是小明对所调查结果的条形统计图.
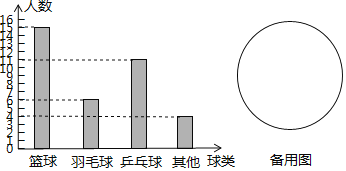
(1)问七年级(1)班共有多少学生?
(2)请你改用扇形统计图来表示我校七年级(1)班同学喜欢的球类运动.
(3)从统计图中你可以获得哪些信息?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了 ![]()
![]() 淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养
淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养 ![]() 天的总成本为
天的总成本为 ![]() 万元;放养
万元;放养 ![]() 天的总成本为
天的总成本为 ![]() 万元(总成本=放养总费用+收购成本).
万元(总成本=放养总费用+收购成本).
(1)设每天的放养费用是 ![]() 万元,收购成本为
万元,收购成本为 ![]() 万元,求
万元,求 ![]() 和
和 ![]() 的值;
的值;
(2)设这批淡水鱼放养 ![]() 天后的质量为
天后的质量为 ![]() (
( ![]() ),销售单价为
),销售单价为 ![]() 元/
元/ ![]() .根据以往经验可知:
.根据以往经验可知: ![]() 与
与 ![]() 的函数关系为
的函数关系为 ![]() ;
; ![]() 与
与 ![]() 的函数关系如图所示.
的函数关系如图所示.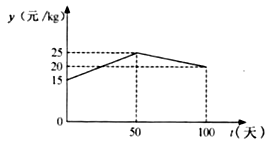
①分别求出当 ![]() 和
和 ![]() 时,
时, ![]() 与
与 ![]() 的函数关系式;
的函数关系式;
②设将这批淡水鱼放养 ![]() 天后一次性出售所得利润为
天后一次性出售所得利润为 ![]() 元,求当
元,求当 ![]() 为何值时,
为何值时, ![]() 最大?并求出最大值.(利润=销售总额-总成本)
最大?并求出最大值.(利润=销售总额-总成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,∠ABC=2∠C,BE平分∠ABC交AC于E,AD⊥BE于D,下列结论:①AC﹣BE=AE;②点E在线段BC的垂直平分线上;③∠DAE=∠C;④BC=4AD,其中正确的有( )
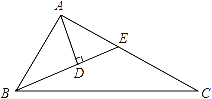
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=30°,将△ABC绕点B旋转α(0<α<60°)到△A′BC′,边AC和边A′C′相交于点P,边AC和边BC′相交于Q.当△BPQ为等腰三角形时,则α=__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com