
【题目】已知:如图所示,∠5=∠CDA=∠ABC,∠1=∠4,∠2=∠3,∠BAD+∠CDA=180°,填空:

∵∠5=∠CDA(已知),∴________∥________(内错角相等,两直线平行).
∵∠5=∠ABC(已知),∴________∥________(同位角相等,两直线平行).
∵∠2=∠3(已知),∴________∥________(内错角相等,两直线平行).
∵∠BAD+∠CDA=180°(已知),
∴________∥________(同旁内角互补,两直线平行).
∵∠5=∠CDA(已知),
又∠5与∠BCD互补,
∠CDA与________互补,
∴∠BCD=∠6(等角的补角相等),
∴________∥________(同位角相等,两直线平行).
【答案】AD BC AB CD AB CD AB CD ∠6 AD BC
【解析】
根据平行线的判定方法求解.
∵∠5=∠CDA(已知),
∴AD∥BC(内错角相等,两直线平行),
∵∠5=∠ABC(已知),
∴AB∥CD(同位角相等,两直线平行),
∵∠2=∠3(已知),
∴AB∥CD(内错角相等,两直线平行),
∵∠BAD+∠CDA=180°(已知),
∴AB∥CD(同旁内角互补,两直线平行),
∵∠5=∠CDA(已知),
∠5与∠BCD互补(邻补角定义),
∠CDA与∠6互补(邻补角定义),
∴∠BCD=∠6 (等量代换),
∴AD∥BC(同位角相等,两直线平行).
故答案为:AD、BC、AB、CD、AB、CD、AB、CD、∠6、AD、BC


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点P在双曲线y= ![]() 上,以P为圆心的⊙P与两坐标轴都相切,E为y轴负半轴上的一点,PF⊥PE交x轴于点F,则OF﹣OE的值是( )
上,以P为圆心的⊙P与两坐标轴都相切,E为y轴负半轴上的一点,PF⊥PE交x轴于点F,则OF﹣OE的值是( ) 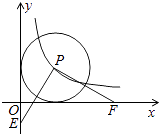
A.6
B.5
C.4
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】取一副三角板按如图所示拼接,固定三角板ADC,将三角板ABC绕点A顺时针方向旋转,旋转角度为α(0°<α≤45°),得到△ABC′.
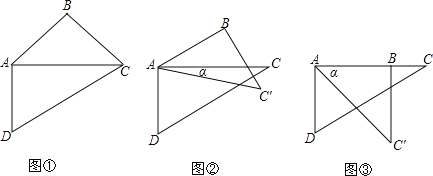
①当α为多少度时,AB∥DC?
②当旋转到图③所示位置时,α为多少度?
③连接BD,当0°<α≤45°时,探求∠DBC′+∠CAC′+∠BDC值的大小变化情况,并给出你的证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.
(1)在方程①3x-1=0,② ![]() ③x-(3x+1)=-5 中,不等组
③x-(3x+1)=-5 中,不等组![]() 的关联方程是________
的关联方程是________
(2)若不等式组 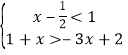 的一个关联方程的根是整数, 则这个关联方程可以是________(写出一个即可)
的一个关联方程的根是整数, 则这个关联方程可以是________(写出一个即可)
(3)若方程 3-x=2x,3+x= ![]() 都是关于 x 的不等式组
都是关于 x 的不等式组 ![]() 的关联方程,直接写出 m 的取值范围.
的关联方程,直接写出 m 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是( )

A. ![]() B. 4 C.
B. 4 C. ![]() D. 5
D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,交OE于点F.
(1)求证:OD=OC;
(2)若∠AOB=60°,求证:OE=4EF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ABC 三个顶点的坐标分别为 A(2, 3) 、B(6, 0) 、C(1, 0)
(1)画ABC ,直接写出ABC 的面积 ;
(2)若A2 BC 与ABC 面积相等,则满足条件的点 A2 有 个,它们的横坐标为 ,纵坐标为 ;
(3)若A3 BC 与ABC 全等,请写出满足条件的 A3 的坐标.
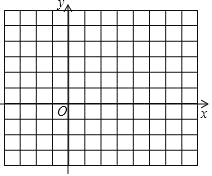
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
∵![]() ,
,![]() ,
,![]() ,……
,……![]() ,
,
∴![]()
=![]()
=![]() =
=![]() .
.
解答下列问题:
(1)在和式![]() 中,第6项为______,第n项是__________.
中,第6项为______,第n项是__________.
(2)上述求和的想法是通过逆用________法则,将和式中的各分数转化为两个数之差,使得除首末两项外的中间各项可以_______,从而达到求和的目的.
(3)受此启发,请你解下面的方程:
![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com