
【题目】取一副三角板按如图所示拼接,固定三角板ADC,将三角板ABC绕点A顺时针方向旋转,旋转角度为α(0°<α≤45°),得到△ABC′.
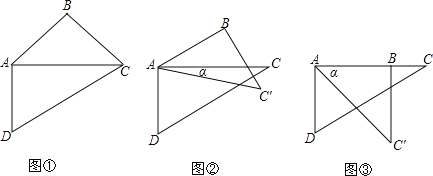
①当α为多少度时,AB∥DC?
②当旋转到图③所示位置时,α为多少度?
③连接BD,当0°<α≤45°时,探求∠DBC′+∠CAC′+∠BDC值的大小变化情况,并给出你的证明.
【答案】(1)当α=15°时,AB∥DC;(2)α=45°;(3)详见解析.
【解析】
(1)若AB∥DC,则∠BAC=∠C=30°,得到α=∠BAC′-∠BAC=45°-30°=15°;
(2)当旋转到图③所示位置时,α=45°,
(3)连接CC′,BD,BO,在△BDO和△OCC′中,利用三角形内角和定理得到∠BDO+∠DBO=∠OCC′+∠OC′C,即可求得∠DBC′+∠CAC′+∠BDC=105°,即得到∠DBC′+∠CAC′+∠BDC值的大小不变.
解:(1)当α=15°时,AB∥DC.
(2)当旋转到图③所示位置时,α=45°.
(3)当0°<α≤45°时,∠DBC′+∠CAC′+∠BDC值的大小不变.
证明:连接CC′,在△BDO和△OCC′中,对顶角∠BOD=∠COC′,
∴∠1+∠2=∠3+∠4,.
∴∠DBC′+∠CAC′+∠BDC
=∠2+∠α+∠1
=180°―∠ACD―∠AC′B
=180°―45°―30°
=105°
∴当0°<α≤45°时,∠DBC′+∠CAC′+∠BDC值的大小不变


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
【题目】某职业高中机电班共有学生42人,其中男生人数比女生人数的2倍少3人.
(1)该班男生和女生各有多少人?
(2)某工厂决定到该班招录30名学生,经测试,该班男、女生每天能加工的零件数分别为50个和45个,为保证他们每天加工的零件总数不少于1460个,那么至少要招录多少名男学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区超市一段时间每天订购面包进行销售,每售出1个面包获利润0.5元,未售出的每个亏损0.3元.
(1)若该超市每天订购面包80个,今后每天售出的面包个数用x(0<x≤80)表示,每天销售面包的利润用y(元)表示,请用含x的式子表示y;
(2)小明连续m天对该超市的面包销量进行统计,并制成了频数分布直方图(每组含最小值,不含最大值)和扇形统计图,如图所示.请根据两图提供的信息计算在m天内日销售利润少于32元的天数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空,完成下列说理过程
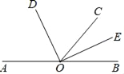
如图,已知点A,O,B在同一条直线上,OE平分∠BOC,∠DOE=90°
求证:OD是∠AOC的平分线;
证明:如图,因为OE是∠BOC的平分线,
所以∠BOE=∠COE.( )
因为∠DOE=90°
所以∠DOC+∠ =90°
且∠DOA+∠BOE=180°﹣∠DOE= °.
所以∠DOC+∠ =∠DOA+∠BOE.
所以∠ =∠ .
所以OD是∠AOC的平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】潜山市某村办工厂,今年前5个月生产某种产品的总量C(件)关于时间t(月)的函数图象如图所示,则该厂对这种产品来说( )

A. 1月至3月每月生产总量逐月增加,4、5两月每月生产总量逐月减少
B. 1月至3月每月生产总量逐月增加,4,5两月每月生产量与3月持平
C. 1月至3月每月生产总量逐月增加,4、5两月均停止生产
D. 1月至3月每月生产总量不变,4、5两月均停止生产
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2 ![]() 的正方形ABCD中,点E是CD边的中点,延长BC至点F,使CF=CE,连接BE,DF.将△BEC绕点C按顺时针方向旋转.当点E恰好落在DF上的点H处时,连接AG、DG、BG,则AG的长是.
的正方形ABCD中,点E是CD边的中点,延长BC至点F,使CF=CE,连接BE,DF.将△BEC绕点C按顺时针方向旋转.当点E恰好落在DF上的点H处时,连接AG、DG、BG,则AG的长是.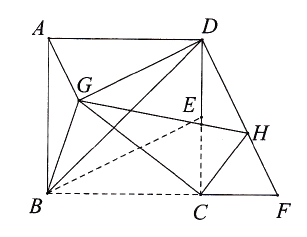
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为∠BAC的外角平分线上一点并且满足BD=CD,∠DBC=∠DCB,过D作DE⊥AC于E,DF⊥AB交BA的延长线于F,则下列结论:

①△CDE≌△BDF;②CE=AB+AE;③∠BDC=∠BAC;④∠DAF=∠CBD.
其中正确的结论有( ).
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,∠5=∠CDA=∠ABC,∠1=∠4,∠2=∠3,∠BAD+∠CDA=180°,填空:

∵∠5=∠CDA(已知),∴________∥________(内错角相等,两直线平行).
∵∠5=∠ABC(已知),∴________∥________(同位角相等,两直线平行).
∵∠2=∠3(已知),∴________∥________(内错角相等,两直线平行).
∵∠BAD+∠CDA=180°(已知),
∴________∥________(同旁内角互补,两直线平行).
∵∠5=∠CDA(已知),
又∠5与∠BCD互补,
∠CDA与________互补,
∴∠BCD=∠6(等角的补角相等),
∴________∥________(同位角相等,两直线平行).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,∠ABC=2∠C,BE平分∠ABC交AC于E,AD⊥BE于D,下列结论:①AC﹣BE=AE;②点E在线段BC的垂直平分线上;③∠DAE=∠C;④BC=4AD,其中正确的有( )
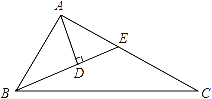
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com