
【题目】如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,交OE于点F.
(1)求证:OD=OC;
(2)若∠AOB=60°,求证:OE=4EF.

【答案】(1)详见解析;(2)详见解析.
【解析】
(1)利用角平分线定理得到ED=EC,再由斜边为公共边,利用HL得到直角三角形ODE与直角三角形OCE全等,利用全等三角形的对应边相等即可得证;
(2)由OE为角平分线,且∠AOB=60°,得到∠DOE=∠EDF=30°,在直角三角形ODE中,利用30度角所对的直角边等于斜边的一半得到OE=2DE,在直角三角形DEF中,利用30度角所对的直角边等于斜边的一半得到DE=2EF,等量代换即可得证.
证明:(1)∵E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,
∴ED=EC,
在Rt△ODE和Rt△OCE中,
![]() ,
,
∴Rt△ODE≌Rt△OCE(HL),
∴OD=OC;
(2)∵∠AOB=60°,OE平分∠AOB,
∴∠DOE=∠COE=30°,
∴∠DEO=60°,∠EDF=30°,
∵在Rt△ODE中,∠DOE=30°,
∴OE=2DE,
∵在Rt△DEF中,∠EDF=30°,
∴DE=2EF,
∴OE=4EF.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】绵阳农科所为了考察某种水稻穗长的分布情况,在一块试验田里随机抽取了50个谷穗作为样本,量得它们的长度(单位:cm).对样本数据适当分组后,列出了如下频数分布表:
穗长 | 4.5≤x<5 | 5≤x<5.5 | 5.5≤x<6 | 6≤x<6.5 | 6.5≤x<7 | 7≤x<7.5 |
频数 | 4 | 8 | 12 | 13 | 10 | 3 |
(1)在图1、图2中分别出频数分布直方图和频数折线图;
(2)请你对这块试验田里的水稻穗长进行分析;并计算出这块试验田里穗长在5.5≤x<7范围内的谷穗所占的百分比.
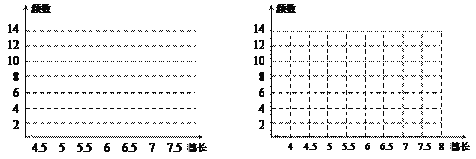
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2 ![]() 的正方形ABCD中,点E是CD边的中点,延长BC至点F,使CF=CE,连接BE,DF.将△BEC绕点C按顺时针方向旋转.当点E恰好落在DF上的点H处时,连接AG、DG、BG,则AG的长是.
的正方形ABCD中,点E是CD边的中点,延长BC至点F,使CF=CE,连接BE,DF.将△BEC绕点C按顺时针方向旋转.当点E恰好落在DF上的点H处时,连接AG、DG、BG,则AG的长是.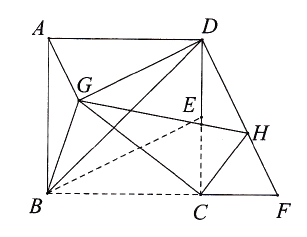
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市计划购进一批甲、乙两种玩具,已知5件甲种玩具的进价与3件乙种玩具的进价的和为231元,2件甲种玩具的进价与3件乙种玩具的进价的和为141元.
(1)求每件甲种、乙种玩具的进价分别是多少元;
(2)近期批发商有优惠活动,如图所示,如果超市决定在甲、乙两种玩具中选购其中一种,且数量超过20件,请你帮助超市判断购进哪种玩具更省钱.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,∠5=∠CDA=∠ABC,∠1=∠4,∠2=∠3,∠BAD+∠CDA=180°,填空:

∵∠5=∠CDA(已知),∴________∥________(内错角相等,两直线平行).
∵∠5=∠ABC(已知),∴________∥________(同位角相等,两直线平行).
∵∠2=∠3(已知),∴________∥________(内错角相等,两直线平行).
∵∠BAD+∠CDA=180°(已知),
∴________∥________(同旁内角互补,两直线平行).
∵∠5=∠CDA(已知),
又∠5与∠BCD互补,
∠CDA与________互补,
∴∠BCD=∠6(等角的补角相等),
∴________∥________(同位角相等,两直线平行).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探索新知)
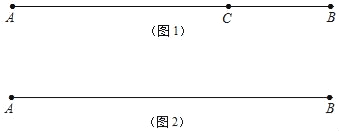
如图1,点C在线段AB上,图中共有3条线段:AB、AC和BC,若其中有一条线段的长度是另一条线段长度的两倍,则称点C是线段AB的“二倍点”.
(1)一条线段的中点 这条线段的“二倍点”;(填“是”或“不是”)
(深入研究)
如图2,若线段AB=20cm,点M从点B的位置开始,以每秒2cm的速度向点A运动,当点M到达点A时停止运动,运动的时间为t秒.
(2)问t为何值时,点M是线段AB的“二倍点”;
(3)同时点N从点A的位置开始,以每秒1cm的速度向点B运动,并与点M同时停止.请直接写出点M是线段AN的“二倍点”时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)a3(-b3)2+(-2ab2)3;
(2)(a-b)10÷(b-a)3÷(b-a)3;
(3)-22+(-![]() )-2-(π-5)0-|-4|;
)-2-(π-5)0-|-4|;
(4)(x+y-3)(x-y+3);
(5)3x2y(2x-3y)-(2xy+3y2)(3x2-3y);
(6)(x-2y)(x+2y)-(x-2y)2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了 ![]()
![]() 淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养
淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养 ![]() 天的总成本为
天的总成本为 ![]() 万元;放养
万元;放养 ![]() 天的总成本为
天的总成本为 ![]() 万元(总成本=放养总费用+收购成本).
万元(总成本=放养总费用+收购成本).
(1)设每天的放养费用是 ![]() 万元,收购成本为
万元,收购成本为 ![]() 万元,求
万元,求 ![]() 和
和 ![]() 的值;
的值;
(2)设这批淡水鱼放养 ![]() 天后的质量为
天后的质量为 ![]() (
( ![]() ),销售单价为
),销售单价为 ![]() 元/
元/ ![]() .根据以往经验可知:
.根据以往经验可知: ![]() 与
与 ![]() 的函数关系为
的函数关系为 ![]() ;
; ![]() 与
与 ![]() 的函数关系如图所示.
的函数关系如图所示.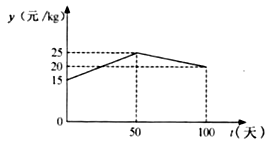
①分别求出当 ![]() 和
和 ![]() 时,
时, ![]() 与
与 ![]() 的函数关系式;
的函数关系式;
②设将这批淡水鱼放养 ![]() 天后一次性出售所得利润为
天后一次性出售所得利润为 ![]() 元,求当
元,求当 ![]() 为何值时,
为何值时, ![]() 最大?并求出最大值.(利润=销售总额-总成本)
最大?并求出最大值.(利润=销售总额-总成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知DE∥BC, AB∥CD,E为AB的中点,∠A=∠B.下列结论:①CD=AE;②AC=DE;③AC平分∠BCD;④O点是DE的中点;⑤AC=AB.其中正确的是( )
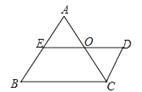
A. ①②④ B. ①③⑤ C. ②③④ D. ②④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com