
【题目】计算:
(1)a3(-b3)2+(-2ab2)3;
(2)(a-b)10÷(b-a)3÷(b-a)3;
(3)-22+(-![]() )-2-(π-5)0-|-4|;
)-2-(π-5)0-|-4|;
(4)(x+y-3)(x-y+3);
(5)3x2y(2x-3y)-(2xy+3y2)(3x2-3y);
(6)(x-2y)(x+2y)-(x-2y)2.
【答案】(1)-7a3b6;(2)(a-b)4;(3)-5;(4)x2-y2-9+6y;(5)-18x2y2+6xy2+9y3;(6)-8y2+4xy.
【解析】
试题分析:(1)原式利用幂的乘方与积的乘方运算法则计算,合并即可得到结果;
(2)原式变形后,利用同底数幂的除法法则计算即可得到结果;
(3)原式利用负指数幂,零指数幂以及绝对值的代数意义化简,计算即可得到结果;
(4)原式利用平方差公式化简,再利用完全平方公式展开即可得到结果;
(5)原式利用单项式乘以多项式法则,以及多项式乘以多项式法则计算,去括号合并即可得到结果;
(6)原式利用平方差公式及完全平方公式化简,去括号合并即可得到结果.
试题解析:(1)原式=a3b6-8a3b6=-7a3b6;
(2)原式=(a-b)10÷(a-b)3÷(a-b)3=(a-b)4;
(3)原式=-4+4-1-4=-5;
(4)原式=x2-(y-3)2=x2-y2-9+6y;
(5)原式=6x3y-9x2y2-6x3y+6xy2-9x2y2+9y3=-18x2y2+6xy2+9y3;
(6)原式=x2-4y2-x2+4xy-4y2=-8y2+4xy.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】问题情境:如图①,在△ABD与△CAE中,BD=AE,∠DBA=∠EAC,AB=AC,易证:△ABD≌△CAE.(不需要证明)
特例探究:如图②,在等边△ABC中,点D、E分别在边BC、AB上,且BD=AE,AD与CE交于点F.求证:△ABD≌△CAE.
归纳证明:如图③,在等边△ABC中,点D、E分别在边CB、BA的延长线上,且BD=AE.△ABD与△CAE是否全等?如果全等,请证明;如果不全等,请说明理由.
拓展应用:如图④,在等腰三角形中,AB=AC,点O是AB边的垂直平分线与AC的交点,点D、E分别在OB、BA的延长线上.若BD=AE,∠BAC=50°,∠AEC=32°,求∠BAD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.
(1)在方程①3x-1=0,② ![]() ③x-(3x+1)=-5 中,不等组
③x-(3x+1)=-5 中,不等组![]() 的关联方程是________
的关联方程是________
(2)若不等式组 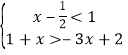 的一个关联方程的根是整数, 则这个关联方程可以是________(写出一个即可)
的一个关联方程的根是整数, 则这个关联方程可以是________(写出一个即可)
(3)若方程 3-x=2x,3+x= ![]() 都是关于 x 的不等式组
都是关于 x 的不等式组 ![]() 的关联方程,直接写出 m 的取值范围.
的关联方程,直接写出 m 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,交OE于点F.
(1)求证:OD=OC;
(2)若∠AOB=60°,求证:OE=4EF.

查看答案和解析>>
科目:初中数学 来源: 题型:
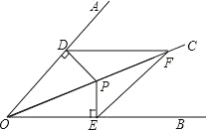
【题目】如图, OC 是AOB 的平分线, P 是OC 上的一点, PD OA 于 D ,PE OB 于 E . F 是OC 上的另一点,连接 DF 、 EF .
(1)求证: DPF EPF ;
(2)比较 DF 与 EF 的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
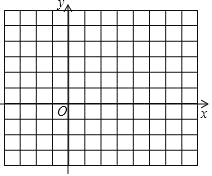
【题目】如图,已知ABC 三个顶点的坐标分别为 A(2, 3) 、B(6, 0) 、C(1, 0)
(1)画ABC ,直接写出ABC 的面积 ;
(2)若A2 BC 与ABC 面积相等,则满足条件的点 A2 有 个,它们的横坐标为 ,纵坐标为 ;
(3)若A3 BC 与ABC 全等,请写出满足条件的 A3 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点(﹣1,y1),(4,y2)在一次函数y=3x﹣2的图象上,则y1 , y2 , 0的大小关系是( )
A.0<y1<y2
B.y1<0<y2
C.y1<y2<0
D.y2<0<y1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地的距离是80千米,一辆公共汽车从A地驶出3小时后,一辆小汽车也从A地出发,它的速度是公共汽车的3倍,已知小汽车比公共汽车迟20分钟到达B地,求两车的速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com