
【题目】如图, OC 是AOB 的平分线, P 是OC 上的一点, PD OA 于 D ,PE OB 于 E . F 是OC 上的另一点,连接 DF 、 EF .
(1)求证: DPF EPF ;
(2)比较 DF 与 EF 的大小关系,并说明理由.
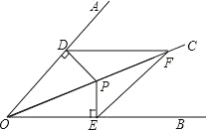
【答案】(1)详见解析;(2)DF=EF,理由详见解析.
【解析】
(1)先根据角平分线的性质可以得出PD=PE,就可以得出△PDO≌△PEO,就可以得出OPD OPE,进而证明DPF EPF ;
(2)根据(1)中△PDO≌△PEO,根据全等三角形的性质得到,OD=OE,∠POD=∠POE,证明△DOF≌△EOF,就可以得出结论.
证明:(1)∵OC是∠AOB的角平分线,PD⊥OA,PE⊥OB,
∴PD=PE.![]()
在Rt△PDO和Rt△PEO中,
![]()
∴Rt△PDO≌Rt△PEO(HL),
OPD OPE,
∴DPF EPF ;
(2)DF=EF.
理由如下:Rt△PDO≌Rt△PEO(HL),
∴OD=OE,∠POD=∠POE.
在△DOF和△EOF中,
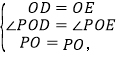
∴△DOF≌△EOF(SAS),
∴DF=EF.


科目:初中数学 来源: 题型:
【题目】学生在素质教育基地进行社会实践活动,帮助农民伯伯采摘了黄瓜和茄子共40kg,了解到这些蔬菜的种植成本共42元,还了解到如下信息:

(1)请问采摘的黄瓜和茄子各多少千克?
(2)这些采摘的黄瓜和茄子可赚多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市计划购进一批甲、乙两种玩具,已知5件甲种玩具的进价与3件乙种玩具的进价的和为231元,2件甲种玩具的进价与3件乙种玩具的进价的和为141元.
(1)求每件甲种、乙种玩具的进价分别是多少元;
(2)近期批发商有优惠活动,如图所示,如果超市决定在甲、乙两种玩具中选购其中一种,且数量超过20件,请你帮助超市判断购进哪种玩具更省钱.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探索新知)
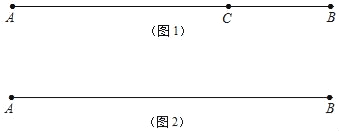
如图1,点C在线段AB上,图中共有3条线段:AB、AC和BC,若其中有一条线段的长度是另一条线段长度的两倍,则称点C是线段AB的“二倍点”.
(1)一条线段的中点 这条线段的“二倍点”;(填“是”或“不是”)
(深入研究)
如图2,若线段AB=20cm,点M从点B的位置开始,以每秒2cm的速度向点A运动,当点M到达点A时停止运动,运动的时间为t秒.
(2)问t为何值时,点M是线段AB的“二倍点”;
(3)同时点N从点A的位置开始,以每秒1cm的速度向点B运动,并与点M同时停止.请直接写出点M是线段AN的“二倍点”时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)a3(-b3)2+(-2ab2)3;
(2)(a-b)10÷(b-a)3÷(b-a)3;
(3)-22+(-![]() )-2-(π-5)0-|-4|;
)-2-(π-5)0-|-4|;
(4)(x+y-3)(x-y+3);
(5)3x2y(2x-3y)-(2xy+3y2)(3x2-3y);
(6)(x-2y)(x+2y)-(x-2y)2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, AC BC , BD AD ,垂足分别为C 、D , AC BD , AC 、BD 交于O
(1)求证: CAB DBA ;
(2)求证: SADO SBCO .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了 ![]()
![]() 淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养
淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养 ![]() 天的总成本为
天的总成本为 ![]() 万元;放养
万元;放养 ![]() 天的总成本为
天的总成本为 ![]() 万元(总成本=放养总费用+收购成本).
万元(总成本=放养总费用+收购成本).
(1)设每天的放养费用是 ![]() 万元,收购成本为
万元,收购成本为 ![]() 万元,求
万元,求 ![]() 和
和 ![]() 的值;
的值;
(2)设这批淡水鱼放养 ![]() 天后的质量为
天后的质量为 ![]() (
( ![]() ),销售单价为
),销售单价为 ![]() 元/
元/ ![]() .根据以往经验可知:
.根据以往经验可知: ![]() 与
与 ![]() 的函数关系为
的函数关系为 ![]() ;
; ![]() 与
与 ![]() 的函数关系如图所示.
的函数关系如图所示.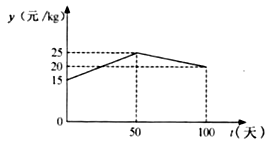
①分别求出当 ![]() 和
和 ![]() 时,
时, ![]() 与
与 ![]() 的函数关系式;
的函数关系式;
②设将这批淡水鱼放养 ![]() 天后一次性出售所得利润为
天后一次性出售所得利润为 ![]() 元,求当
元,求当 ![]() 为何值时,
为何值时, ![]() 最大?并求出最大值.(利润=销售总额-总成本)
最大?并求出最大值.(利润=销售总额-总成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
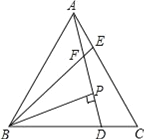
【题目】如图,已知△ABC为等边三角形,AE=CD,AD、BE相交于点F.
(1)求证:△ABE≌△CAD;
(2)若BP⊥AD于点P,PF=9,EF=3,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC在平面直角坐标系中的位置如图所示.
(1)把△ABC向下平移2个单位长度得到△A1B1C1,请画出△A1B1C1;
(2)请画出△A1B1C1关于y轴对称的△A2B2C2,并写出A2的坐标;
(3)求△ABC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com