
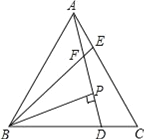
【题目】如图,已知△ABC为等边三角形,AE=CD,AD、BE相交于点F.
(1)求证:△ABE≌△CAD;
(2)若BP⊥AD于点P,PF=9,EF=3,求AD的长.
【答案】(1)证明见解析;(2)AD=21.
【解析】试题分析:(1)根据等边三角形的性质得出AB=AC,∠BAE=∠ACD,结合AE=CD得出三角形全等;(2)根据全等得出BE=AD,∠ABE=∠CAD,结合外角的性质得出∠BFP=60°,然后根据直角三角形的性质得出BF的长度,最后根据AD=BE=BF+EF得出答案.
试题解析:(1)∵△ABC为等边三角形,∴AB=AC,∠BAE=∠ACD,又∵AE=CD,
∴△ABE≌△CAD;
(2)∵△ABE≌△CAD, ∴BE=AD,∠ABE=∠CAD,
∴∠ABE+∠BAP=∠CAD+∠BAP, 即∠BFP=∠BAC=60°,
又∵BP⊥AD,∴∠BPF=90°, ∴∠FBP=30°, ∴BF=2PF=18,
∴AD=BE=BF+EF=18+3=21.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源: 题型:
【题目】如图甲所示,是小亮设计的一种智力拼图玩具的一部分,已知AB∥CD,∠B=30°,∠BEC=62°,求∠C的度数. 
(1)填写根据:过点E作EF∥AB,如图甲所示, ∵AB∥DC,EF∥AB,
∴EF∥DC()
∴∠B=∠BEF()
∠C=∠CEF()
∴∠B+∠C=∠BEF+∠CEF
即∠B+∠C=∠BEC
∴∠C=∠BEC﹣∠B=62°﹣30°=32°
(2)方法迁移:如图乙,已知AE∥CD,若∠DCB=135°,∠ABC=72°,试求∠BAE的度数. 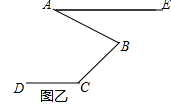
查看答案和解析>>
科目:初中数学 来源: 题型:
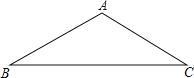
【题目】如图,在△ABC中,AB=AC=8cm,∠BAC=120°.
(1)作△ABC的外接圆(只需作出图形,并保留作图痕迹);
(2)求它的外接圆半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
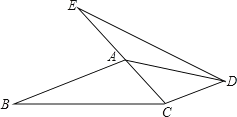
【题目】已知:如图,点E、A、C在同一条直线上,AB∥CD,AB=CE,∠B=∠E.
(1)求证:△ABC≌△CED;
(2)若∠B=25°,∠ACB=45°,求∠ADE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中是必然发生的事件是( )
A.抛两枚均匀的硬币,硬币落地后,都是正面朝上
B.射击运动员射击一次,命中十环
C.在地球上,抛出的篮球会下落
D.明天会下雨
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com