
【题目】如图甲所示,是小亮设计的一种智力拼图玩具的一部分,已知AB∥CD,∠B=30°,∠BEC=62°,求∠C的度数. 
(1)填写根据:过点E作EF∥AB,如图甲所示, ∵AB∥DC,EF∥AB,
∴EF∥DC()
∴∠B=∠BEF()
∠C=∠CEF()
∴∠B+∠C=∠BEF+∠CEF
即∠B+∠C=∠BEC
∴∠C=∠BEC﹣∠B=62°﹣30°=32°
(2)方法迁移:如图乙,已知AE∥CD,若∠DCB=135°,∠ABC=72°,试求∠BAE的度数. 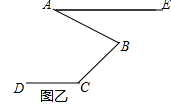
【答案】
(1)两条直线都与第三条直线平行,那么这两条直线平行;两直线平行,内错角相等;两直线平行,内错角相等
(2)解:如图,过B作BF∥AE,
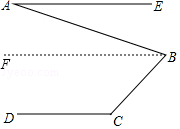
∵AE∥CD,
∴BF∥CD,
∴∠DCB+∠CBF=180°,∠BAE=∠ABF,
∵∠DCB=135°,
∴∠CBF=180°﹣135°=45°,
∵∠ABC=72°,
∴∠ABF=∠ABC﹣∠CBF=72°﹣45°=27°,
∴∠BAE=27°
【解析】解:(1)∵AB∥DC,EF∥AB, ∴EF∥DC(两条直线都与第三条直线平行,那么这两条直线平行 )
∴∠B=∠BEF( 两直线平行,内错角相等)
∠C=∠CEF( 两直线平行,内错角相等 )
∴∠B+∠C=∠BEF+∠CEF
即∠B+∠C=∠BEC
∴∠C=∠BEC﹣∠B=62°﹣30°=32°;
所以答案是:两条直线都与第三条直线平行,那么这两条直线平行; 两直线平行,内错角相等; 两直线平行,内错角相等.
【考点精析】认真审题,首先需要了解平行线的判定与性质(由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质).


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
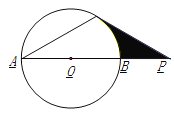
【题目】如图,已知:⊙O的直径AB与弦AC的夹角∠A=30°,AC=CP.
(1) 求证:CP是⊙O的切线;
(2) 若PC=6,AB=4![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学规定学生的学期体育成绩满分为100分,其中早锻炼及体育课外活动占20%,期中考试成绩占30%,期末考试成绩占50%.小桐的三项成绩(百分制)依次为95,90,85.则小桐这学期的体育成绩是( )
A. 88.5B. 86.5C. 90D. 90.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大众创业,万众创新,据不完全统计,2015年毕业的大学生中创业人数已经达到7490000人,将7490000这个数据用科学记数法表示为( )
A.7.49×107
B.7.49×106
C.74.9×106
D.0.749×107
查看答案和解析>>
科目:初中数学 来源: 题型:
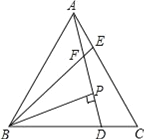
【题目】如图,已知△ABC为等边三角形,AE=CD,AD、BE相交于点F.
(1)求证:△ABE≌△CAD;
(2)若BP⊥AD于点P,PF=9,EF=3,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com