
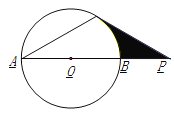
【题目】如图,已知:⊙O的直径AB与弦AC的夹角∠A=30°,AC=CP.
(1) 求证:CP是⊙O的切线;
(2) 若PC=6,AB=4![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
【答案】(1)、证明过程见解析;(2)、6![]() -2π
-2π
【解析】
试题分析:(1)、连接OC,根据∠A的度数以及AC=CP得出∠A=∠P=30°,根据OC=OA得出∠COP=60°,从而得到∠OCP的度数;(2)、根据AB的长度得出OC和OB的长度,从而求出扇形OBC的面积,然后利用△PCO的面积减去扇形OBC的面积得到阴影部分的面积.
试题解析:(1)、连结OC ∵∠A=30°,AC=CP ∴∠P=∠A=30° ∵OC=OA
∴∠COP=2∠A=60° ∴∠OCP=90° ∴OC⊥PC ∴PC是⊙O的切线
(2)、∵AB=4![]() ∴OC=OB=2
∴OC=OB=2![]() ∴S扇OBC=2
∴S扇OBC=2![]()
S![]() =S△PCO-S扇OBC =6
=S△PCO-S扇OBC =6![]() -2
-2![]()


科目:初中数学 来源: 题型:
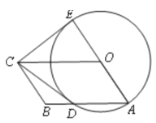
【题目】如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长 AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题:
(1)求证:CD是⊙O的切线;
(2)若平行四边形OABC的两边长是方程![]() 的两根,求平行四边形OABC的面积.
的两根,求平行四边形OABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“五一”期间,小明、小亮等同学随家长一同到某公园游玩,下面是购买门票时,小明与他爸爸的对话(如图),试根据图中的信息, 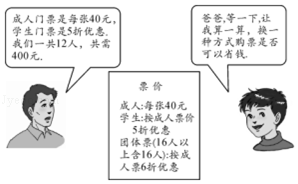
解答下列问题:
(1)他们共去了几个成人,几个学生?
(2)请你帮助算算,用哪种方式购票更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图甲所示,是小亮设计的一种智力拼图玩具的一部分,已知AB∥CD,∠B=30°,∠BEC=62°,求∠C的度数. 
(1)填写根据:过点E作EF∥AB,如图甲所示, ∵AB∥DC,EF∥AB,
∴EF∥DC()
∴∠B=∠BEF()
∠C=∠CEF()
∴∠B+∠C=∠BEF+∠CEF
即∠B+∠C=∠BEC
∴∠C=∠BEC﹣∠B=62°﹣30°=32°
(2)方法迁移:如图乙,已知AE∥CD,若∠DCB=135°,∠ABC=72°,试求∠BAE的度数. 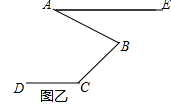
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=8cm,∠BAC=120°.
(1)作△ABC的外接圆(只需作出图形,并保留作图痕迹);
(2)求它的外接圆半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com