
����Ŀ��������������֮��֮�ƣ�ijˮ����ֳ��Ϊ�˸��õط��Ӽ������ƣ�һ�����չ��� ![]()
![]() ��ˮ�㣬�ƻ���ֳһ��ʱ����ٳ��ۣ���֪ÿ������ķ�����ͬ������
��ˮ�㣬�ƻ���ֳһ��ʱ����ٳ��ۣ���֪ÿ������ķ�����ͬ������ ![]() ����ܳɱ�Ϊ
����ܳɱ�Ϊ ![]() ��Ԫ������
��Ԫ������ ![]() ����ܳɱ�Ϊ
����ܳɱ�Ϊ ![]() ��Ԫ���ܳɱ�=�����ܷ���+�չ��ɱ�����
��Ԫ���ܳɱ�=�����ܷ���+�չ��ɱ�����
��1����ÿ��ķ��������� ![]() ��Ԫ���չ��ɱ�Ϊ
��Ԫ���չ��ɱ�Ϊ ![]() ��Ԫ����
��Ԫ���� ![]() ��
�� ![]() ��ֵ��
��ֵ��
��2����������ˮ����� ![]() ��������Ϊ
��������Ϊ ![]() ��
�� ![]() �������۵���Ϊ
�������۵���Ϊ ![]() Ԫ/
Ԫ/ ![]() ���������������֪��
���������������֪�� ![]() ��
�� ![]() �ĺ�����ϵΪ
�ĺ�����ϵΪ ![]() ��
�� ![]() ��
�� ![]() �ĺ�����ϵ��ͼ��ʾ��
�ĺ�����ϵ��ͼ��ʾ��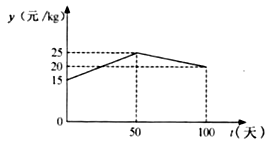
�ٷֱ������ ![]() ��
�� ![]() ʱ��
ʱ�� ![]() ��
�� ![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
���轫������ˮ����� ![]() ���һ���Գ�����������Ϊ
���һ���Գ�����������Ϊ ![]() Ԫ����
Ԫ���� ![]() Ϊ��ֵʱ��
Ϊ��ֵʱ�� ![]() ���������ֵ��������=�����ܶ�-�ܳɱ���
���������ֵ��������=�����ܶ�-�ܳɱ���
���𰸡�
��1��
�⣺����ɵã� ![]()
��� ![]()
��a��ֵΪ0.04��b��ֵΪ30.
��2��
�⣺�ٵ�0��t��50ʱ����y��t�ĺ�����ϵʽΪy=k1t+n1.
�ѵ㣨0��15������50��25��������ֱ�����:![]()
���: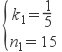
��y��t�ĺ�����ϵʽΪy=![]() t+15.
t+15.
��50��t��100ʱ����y��t�ĺ�����ϵʽΪy=k2t+n2.
�ѵ㣨50��25���ͣ�100��20��������ֱ����� :![]()
��� :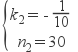
��y��t�ĺ�����ϵʽΪy=-![]() t+30.
t+30.
��������ã���0��t��50ʱ��
W=20000����![]() t+15��-��400t+300000��=3600t
t+15��-��400t+300000��=3600t
��3600��0���൱t=50ʱ��W���ֵ=180000��Ԫ��
��50��t��100ʱ��W=��100t+15000��(-![]() t+30��-��400t+300000��=-10t2+1100t+150000=-10��t-55��2+180250
t+30��-��400t+300000��=-10t2+1100t+150000=-10��t-55��2+180250
��-10��0���൱t=55ʱ��W���ֵ=180250
������������tΪ55��ʱ��W������ֵΪ180250Ԫ.
����������1���������⣬�з�������⼴��.
��2��ͨ��ͼ���ҵ���Ӧ�ĵ�����꣬���ݴ���ϵ���������г������鼴�ɵõ���������ʽ��Ȼ���������=�����ܶ�-�ܳɱ�=���۵��ۡ���������-�������ܷ���+�չ��ɱ�����Ȼ�����һ�κ������ص�Ͷ��κ�������ֵ��⼴��.
�����㾫����������Ҫ�����˽��Ԫһ�η������ȷ��һ�κ����ı���ʽ�����֪ʶ�㣬��Ҫ���ն�Ԫһ�η����飺�ٴ�����Ԫ�����ڼӼ���Ԫ����ȷ��һ��һ�κ�������Ҫȷ��һ�κ�������ʽy=kx+b��k������0���еij���k��b�������������һ�㷽���Ǵ���ϵ����������ȷ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ǹ涨��![]() ��
��![]() ��a��0������a�ĸ�P���ݵ���a��p���ݵĵ���������
��a��0������a�ĸ�P���ݵ���a��p���ݵĵ���������![]() ��
��![]()
��1�����㣺![]() ��__��
��__��![]() ��__��
��__��
��2�����![]() ��
��![]() ����ôp��__�����
����ôp��__�����![]() ��
��![]() ����ôa��__��
����ôa��__��
��3�����![]() ��
��![]() ����a��pΪ������������������a��p��ȡֵ��
����a��pΪ������������������a��p��ȡֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��E����AOB��ƽ������һ�㣬EC��OB��ED��OA��C��D�Ǵ��㣬����CD����OE�ڵ�F��
��1����֤��OD=OC��
��2������AOB=60������֤��OE=4EF��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
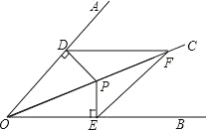
����Ŀ����ͼ�� OC ��AOB ��ƽ���ߣ� P ��OC �ϵ�һ�㣬 PD OA �� D ��PE OB �� E �� F ��OC �ϵ���һ�㣬���� DF �� EF ��
��1����֤�� DPF EPF ��
��2���Ƚ� DF �� EF �Ĵ�С��ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
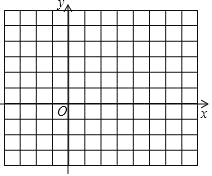
����Ŀ����ͼ����֪ABC �������������ֱ�Ϊ A(2, 3) ��B(6, 0) ��C(1, 0)
��1����ABC ��ֱ��д��ABC ����� ��
��2����A2 BC ��ABC �����ȣ������������ĵ� A2 �� �������ǵĺ�����Ϊ ��������Ϊ ��
��3����A3 BC ��ABC ȫ�ȣ���д������������ A3 �����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
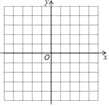
����Ŀ����ƽ��ֱ������ϵ�У���ͼÿ��һ����λ����������и���A����2����1����B��2����1����C��2��2����D��3��2����E��0��3����F����3��2����G����2��2����A����2����1�������ν����������������۲��������ͼ�Σ�����ʲô������ͼ�λش��������⣺
��1��ͼ������Щ�����������ϣ����ǵ�������ʲô�ص㣿
��2���߶�FD��x����ʲôλ�ù�ϵ����F�͵�D��������ʲô�ص㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�㣨��1��y1������4��y2����һ�κ���y=3x��2��ͼ���ϣ���y1 �� y2 �� 0�Ĵ�С��ϵ�ǣ� ��
A.0��y1��y2
B.y1��0��y2
C.y1��y2��0
D.y2��0��y1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
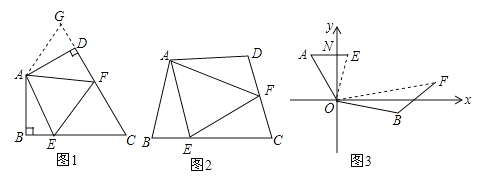
����Ŀ����1�����ⱳ������ͼ1�����ı���ABCD�У�AB��AD����BAD��120�㣬��B����ADC��90�㣬E��F�ֱ���BC��CD�ϵĵ㣬�ҡ�EAF��60�㣬̽��ͼ���߶�BE��EF��FD֮���������ϵ��С��ͬѧ̽��������ķ������ӳ�FD����G��ʹDG��BE������AG����֤����ABE�ա�ADG����֤����AEF�ա�AGF���ɵó����ۣ����Ľ���Ӧ��_____________________��
��2��̽�����죺��ͼ2�������ı���ABCD�У�AB��AD����B����D��180�㣬E��F�ֱ���BC��CD�ϵĵ㣬�ҡ�EAF����BAD�����������Ƿ���Ȼ��������˵�����ɣ�
��3������Ӧ�ã���ͼ3����ij�ξ�����ϰ�У���ͧ����ָ�����ģ�O������ƫ��30���A������ͧ����ָ��������ƫ��70���B������������ͧ��ָ�����ĵľ�����ȣ��ӵ��ж�ָ���ͧ��������������60����/Сʱ���ٶ�ǰ������ͧ���ر�ƫ��50��ķ�����80����/Сʱ���ٶ�ǰ����1.5Сʱ��ָ�����Ĺ۲�ס�������ͧ�ֱ�E��F����������ͧ��ָ������O֮��нǡ�EOF=70�㣬�����ʱ����֮ͧ��ľ��룮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com