
【题目】如图,在Rt△ABC中,∠C=30°,将△ABC绕点B旋转α(0<α<60°)到△A′BC′,边AC和边A′C′相交于点P,边AC和边BC′相交于Q.当△BPQ为等腰三角形时,则α=__________.

【答案】20°或40°
【解析】
过B作BD⊥AC于D,过B作BE⊥A'C'于E,根据旋转可得△ABC≌△A'BC',则BD=BE,进而得到BP平分∠A'PC,再根据∠C=∠C'=30°,∠BQC=∠PQC',可得∠CBQ=∠C'PQ=θ,即可得出∠BPQ=![]() (180°-∠C'PQ)=90°-
(180°-∠C'PQ)=90°-![]() θ,分三种情况讨论,利用三角形内角和等于180°,即可得到关于θ的方程,进而得到结果.
θ,分三种情况讨论,利用三角形内角和等于180°,即可得到关于θ的方程,进而得到结果.
如图,过B作BD⊥AC于D,过B作BE⊥A'C'于E,
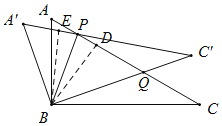
由旋转可得,△ABC≌△A'BC',则BD=BE,
∴BP平分∠A'PC,
又∵∠C=∠C'=30°,∠BQC=∠PQC',
∴∠CBQ=∠C'PQ=θ,
∴∠BPQ=![]() (180°-∠C'PQ)=90°-
(180°-∠C'PQ)=90°-![]() θ,
θ,
分三种情况:
①如图所示,当PB=PQ时,∠PBQ=∠PQB=∠C+∠QBC=30°+θ,
∵∠BPQ+∠PBQ+∠PQB=180°,
∴90°-![]() θ+2×(30°+θ)=180°,
θ+2×(30°+θ)=180°,
解得θ=20°;
②如图所示,当BP=BQ时,∠BPQ=∠BQP,
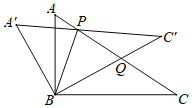
即90°-![]() θ=30°+θ,
θ=30°+θ,
解得θ=40°;
③当QP=QB时,∠QPB=∠QBP=90°-![]() θ,
θ,
又∵∠BQP=30°+θ,
∴∠BPQ+∠PBQ+∠BQP=2(90°-![]() θ)+30°+θ=210°>180°(不合题意),
θ)+30°+θ=210°>180°(不合题意),
故答案为:20°或40°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如果一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.
(1)在方程①3x-1=0,② ![]() ③x-(3x+1)=-5 中,不等组
③x-(3x+1)=-5 中,不等组![]() 的关联方程是________
的关联方程是________
(2)若不等式组 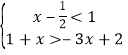 的一个关联方程的根是整数, 则这个关联方程可以是________(写出一个即可)
的一个关联方程的根是整数, 则这个关联方程可以是________(写出一个即可)
(3)若方程 3-x=2x,3+x= ![]() 都是关于 x 的不等式组
都是关于 x 的不等式组 ![]() 的关联方程,直接写出 m 的取值范围.
的关联方程,直接写出 m 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ABC 三个顶点的坐标分别为 A(2, 3) 、B(6, 0) 、C(1, 0)
(1)画ABC ,直接写出ABC 的面积 ;
(2)若A2 BC 与ABC 面积相等,则满足条件的点 A2 有 个,它们的横坐标为 ,纵坐标为 ;
(3)若A3 BC 与ABC 全等,请写出满足条件的 A3 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点(﹣1,y1),(4,y2)在一次函数y=3x﹣2的图象上,则y1 , y2 , 0的大小关系是( )
A.0<y1<y2
B.y1<0<y2
C.y1<y2<0
D.y2<0<y1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=-x+m分别交于x轴、y轴于A,B两点,已知点C(2,0).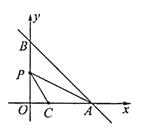
(1)当直线AB经过点C时,点O到直线AB的距离是;
(2)设点P为线段OB的中点,连结PA,PC,若∠CPA=∠ABO,则m的值是.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
∵![]() ,
,![]() ,
,![]() ,……
,……![]() ,
,
∴![]()
=![]()
=![]() =
=![]() .
.
解答下列问题:
(1)在和式![]() 中,第6项为______,第n项是__________.
中,第6项为______,第n项是__________.
(2)上述求和的想法是通过逆用________法则,将和式中的各分数转化为两个数之差,使得除首末两项外的中间各项可以_______,从而达到求和的目的.
(3)受此启发,请你解下面的方程:
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地的距离是80千米,一辆公共汽车从A地驶出3小时后,一辆小汽车也从A地出发,它的速度是公共汽车的3倍,已知小汽车比公共汽车迟20分钟到达B地,求两车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形是将正三角形按一定规律排列,第 1 个图形中所有正三角形的个数有 1 个,第 2 个图形中所有正三角形的个数有 5 个,第 3 个图形中所有正三角形的个数有 17 个,则第 5 个图形中所有正三角形的个数有( )
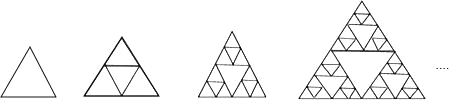
A. 160 B. 161 C. 162 D. 163
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com