
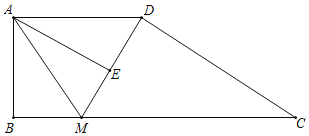
【题目】已知,梯形ABCD中,AD∥BC,∠ABC=90°,AB=3,BC=10,AD=5,M是BC边上的任意一点,联结DM,联结AM.
(1)若AM平分∠BMD,求BM的长;
(2)过点A作AE⊥DM,交DM所在直线于点E.
①设BM=x,AE=y求y关于x的函数关系式;
②联结BE,当△ABE是以AE为腰的等腰三角形时,请直接写出BM的长.
【答案】(1)1或9;(2)①y=![]() .②1或9或4.
.②1或9或4.
【解析】
(1)考虑∠DMB为锐角和钝角两种情况即可解答;
(2) ①作MH⊥AD于H,根据勾股定理,用被开方式含x的二次根式表示DM,根据△ADM面积的两种算法建立等式,即可求出y关于x的函数关系式;②分AB=AE和EA=EB两种情况讨论求解.
解:(1)如图1中,作DH⊥BC于H.则四边形ABHD是矩形,AD=BH=5,AB=DH=3.

当MA平分∠DMB时,易证∠AMB=∠AMD=∠DAM,可得DA=DM=5,
在Rt△DMH中,DM=AD=5,DH=3,
∴MH=![]() =
=![]() =4,
=4,
∴BM=BH-MH=1,
当AM′平分∠BM′D时,同法可证:DA=DM′,HM′=4,
∴BM′=BH+HM′=9.
综上所述,满足条件的BM的值为1或9.
(2)①如图2中,作MH⊥AD于H.

在Rt△DMH中,DM=![]() =
=![]() ,
,
∵S△ADM=![]() ADMH=
ADMH=![]() DMAE,
DMAE,
∴5×3=y![]()
∴y=![]() .
.
②如图3中,当AB=AE时,y=3,此时5×3=3![]() ,
,
解得x=1或9.

如图4中,当EA=EB时,DE=EM,
∵AE⊥DM,
∴DA=AM=5,
在Rt△ABM中,BM=![]() =4.
=4.

综上所述,满足条件的BM的值为1或9或4.
故答案为:(1)1或9;(2)①y=![]() .②1或9或4.
.②1或9或4.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
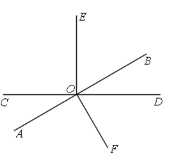
【题目】已知如图,直线AB、CD相交于点O,∠COE=90°,若∠BOD:∠BOC=1:5.
(1)求∠AOC的度数;
(2)如图,过点O作OF⊥AB,求∠DOF与∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=ax+b与双曲线y= ![]() (x>0)交于A(x1 , y1),B(x2 , y2)两点(A与B不重合),直线AB与x轴交于P(x0 , 0),与y轴交于点C.
(x>0)交于A(x1 , y1),B(x2 , y2)两点(A与B不重合),直线AB与x轴交于P(x0 , 0),与y轴交于点C. 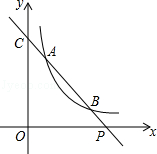
(1)若A,B两点坐标分别为(1,3),(3,y2),求点P的坐标.
(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标.
(3)结合(1),(2)中的结果,猜想并用等式表示x1 , x2 , x0之间的关系(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c与⊙M相交于A、B、C、D四点,其中A、B两点的坐标分别为(﹣1,0),(0,﹣2),点D在x轴上且AD为⊙M的直径.点E是⊙M与y轴的另一个交点,过劣弧 ![]() 上的点F作FH⊥AD于点H,且FH=1.5
上的点F作FH⊥AD于点H,且FH=1.5
(1)求点D的坐标及该抛物线的表达式;
(2)若点P是x轴上的一个动点,试求出△PEF的周长最小时点P的坐标;
(3)在抛物线的对称轴上是否存在点Q,使△QCM是等腰三角形?如果存在,请直接写出点Q的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年怀柔区中考体育加试女子800米耐力测试中,同时起跑的李丽和吴梅所跑的路程![]() 米
米![]() 与所用时间
与所用时间![]() 秒
秒![]() 之间的函数图象分别为线段OA和折线
之间的函数图象分别为线段OA和折线![]() 下列说法正确的是
下列说法正确的是![]()
![]()
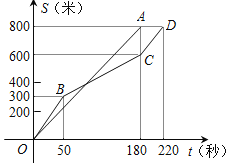
A. 李丽的速度随时间的增大而增大
B. 吴梅的平均速度比李丽的平均速度大
C. 在起跑后180秒时,两人相遇
D. 在起跑后50秒时,吴梅在李丽的前面
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,E、F分别是CD、AB延长线上的点,连结EF,分别交AD、BC于点G、H.若∠1=∠2,∠A=∠C,试说明AD//BC和AB//CD.请完成下面的推理过程,填写理由或数学式:

∵∠1=∠2,∠1=∠AGH(_________)
∴∠2=∠AGH(________)
∴AD//BC(________)
∴∠ADE=∠C(________)
∵∠A=∠C(已知)
∴∠ADE=_______(等量代换)
∴AB//CD(_______)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,则下列结论中不正确的是( )
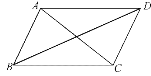
A. 当AB=BC时,四边形ABCD是菱形
B. 当AC⊥BD时,四边形ABCD是菱形
C. 当∠ABC=90°时,四边形ABCD是矩形
D. 当AC=BD时,四边形ABCD是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 平面内,没有公共点的两条线段平行
B. 平面内,没有公共点的两条射线平行
C. 没有公共点的两条直线互相平行
D. 互相平行的两条直线没有公共点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com