
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx+c���M�ཻ��A��B��C��D�ĵ㣬����A��B���������ֱ�Ϊ����1��0������0����2������D��x������ADΪ��M��ֱ������E�ǡ�M��y�����һ�����㣬���ӻ� ![]() �ϵĵ�F��FH��AD�ڵ�H����FH=1.5
�ϵĵ�F��FH��AD�ڵ�H����FH=1.5
��1�����D�����꼰�������ߵı���ʽ��
��2������P��x���ϵ�һ�����㣬�������PEF���ܳ���Сʱ��P�����ꣻ
��3���������ߵĶԳ������Ƿ���ڵ�Q��ʹ��QCM�ǵ��������Σ�������ڣ���ֱ��д����Q�����ꣻ��������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺����BD��
��AD�ǡ�M��ֱ�������ABD=90��
���AOB�ס�ABD��
�� ![]() =
= ![]() ��
��
��Rt��AOB��AO=1��BO=2��
���ݹ��ɶ����ã�AB= ![]() ��
��
�� ![]() ��
��
��AD=5��
��DO=AD��AO=5��1=4��
��D��4��0����
�ѵ�A����1��0����B��0����2����D��4��0������y=ax2+bx+c�ɵã�
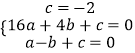 ��
��
��ã� 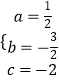 ��
��
�������߱���ʽΪ�� ![]()
��2��
�⣺����FM��
��Rt��FHM��FM= ![]() ��FH=
��FH= ![]() ��
��
��MH= ![]() =2��
=2��
OM=AM��OA= ![]() ��1=
��1= ![]() ��
��
��OH=OM+MH= ![]() +2=
+2= ![]() ��
��
��F�� ![]() ��
�� ![]() ����
����
��ֱ��BF�Ľ���ʽΪy=kx+b��
�� 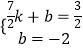 ��
��
��ֱ��BF�Ľ���ʽΪ��y=x��2��
����BF��x���ڵ�P���ߵ�E���B����x��Գƣ�
���P������
��y=0ʱ��x=2��
��P��2��0��
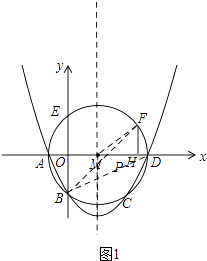
��3��
�⣺��ͼ��CM= ![]()
������ ![]() �ĶԳ���Ϊֱ��x=
�ĶԳ���Ϊֱ��x= ![]() ��
��
��OM= ![]() �����M��ֱ��x=
�����M��ֱ��x= ![]() �ϣ�
�ϣ�
����Բ�ĶԳ��Կ�֪����C���B����ֱ��x= ![]() �Գƣ�
�Գƣ�
���C��3����2����
�ٵ�CM=MQ= ![]() ʱ����Q������x���Ϸ���Ҳ������x���·���
ʱ����Q������x���Ϸ���Ҳ������x���·���
��Q1�� ![]() ��
�� ![]() ����Q2��
����Q2�� ![]() ��
�� ![]() ����
����
�ڵ�CM=CQʱ������C��CN��MQ��
��MN=NQ=2����MQ=4��
��Q3�� ![]() ����4����
����4����
�۵�CQ4=MQ4ʱ������C��CR��MQ��Q4V��CM��
��MV=CV= ![]() ��Q4V=
��Q4V= ![]() ��
��
Rt��CRM��Rt��Q4VM��
�� 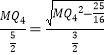 ��
��
��ã�MQ4= ![]() ��
��
��Q4�� ![]() ����
���� ![]() ��
��
���Ͽ�֪�������ĸ��㣬����
Q1�� ![]() ��
�� ![]() ����Q2��
����Q2�� ![]() ��
�� ![]() ����Q3��
����Q3�� ![]() ����4����Q4��
����4����Q4�� ![]() ����
���� ![]() ��
��
����������1�����ȸ���Բ����Գ��������D�����꣬��A��B��D������룬�����������Ĵ𰸣���2�����ڵ�E���B ����x��Գƣ����ԣ�����BF��ֱ��BF��x��Ľ��㣬��Ϊ��P���ݴ˼��ɵý⣻��3����CM=MQ��CM=CQ��MQ=CQ����������з������ݴ˼��ɵý⣮
�����㾫����ͨ��������ö��κ�����ͼ��Ͷ��κ��������ʣ����ն��κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С�����Խ����⣮


 ���⿼����Ԫ���Ծ�ϵ�д�
���⿼����Ԫ���Ծ�ϵ�д� ��У���˳�̾�ϵ�д�
��У���˳�̾�ϵ�д� ��У���һ��ͨϵ�д�
��У���һ��ͨϵ�д� �γ̴����Ծ�����100��ϵ�д�
�γ̴����Ծ�����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
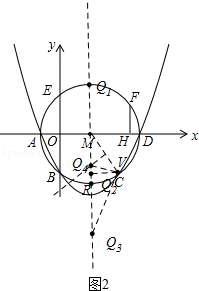
����Ŀ����ͼ����ǡ�ABC����D��E�ֱ���AB��AC���ϵĵ�����ADC�ա�ADC'����AEB�ա�AEB'����C'D��EB'��BC����BE��CD���ڵ�F������BAC��x�㣬���BFC�Ĵ�С��_____�㣮���ú�x��ʽ�ӱ�ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��1������2x3y��2����2xy��+����2x3y��3��2x2
��2��20202��2019��2021
��3������2a+b+1����2a+b��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������ϵ�в���ʽ��
��1��a��1������� ��
��2��a��![]() ��b��
��b��![]() �IJ��Ǹ��� ��
�IJ��Ǹ��� ��
��3��a��b�������͵�ƽ��������9 ��
��4��a��![]() ����b�ĺ͵�ƽ���ǷǸ��� ��
����b�ĺ͵�ƽ���ǷǸ��� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������CΪ��O��һ�㣬AE����C�������ഹֱ������ΪE��AE����O�ڵ�D��ֱ��EC��AB���ӳ����ڵ�P������AC��BC��PB��PC=1��2�� 
��1����֤��ACƽ�֡�BAD��
��2��̽���߶�PB��AB֮���������ϵ����˵�����ɣ�
��3����AD=3�����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
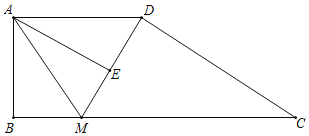
����Ŀ����֪������ABCD�У�AD��BC����ABC=90�㣬AB=3��BC=10��AD=5��M��BC���ϵ�����һ�㣬����DM������AM��
��1����AMƽ�֡�BMD����BM�ij���
��2������A��AE��DM����DM����ֱ���ڵ�E��
����BM=x��AE=y��y����x�ĺ�����ϵʽ��
������BE������ABE����AEΪ���ĵ���������ʱ����ֱ��д��BM�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���Ӽҵ�ͼ��ݿ���Ȼ�أ�����ҵľ���y����ҵ�ʱ��x֮��Ķ�Ӧ��ϵ��ͼ��ʾ�����С����ͼ��ݿ���30���ӣ���ô�����50����ʱ��ҵľ���Ϊ km��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��͵ܵ�С���ֱ�ӼҺ�ͼ���ͬʱ��������ͬһ��·������У�С���ܲ���;��Ϊ���У�����ͼ���ǡ����30 min.С�������г���300 m/min���ٶ�ֱ�ӻؼң�������ҵ�·��y(m)������뿪�����ص�ʱ��x(min)֮��ĺ���ͼ����ͼ9��ʾ��
��1������ͼ���֮���·��Ϊ m��С�Ჽ�е��ٶ�Ϊ m/min��
��2����С����ҵ�·��y����x�ĺ�������ʽ����д���Ա�����ȡֵ��Χ��
��3��������������ʱ�䣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����������У�����֤����ABD�ա�ACD���ǣ�������

A. AB=AC��BD=CD B. ��B=��C��BD=CD
C. ��B=��C����BAD=��CAD D. ��ADB=��ADC��DB=DC
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com