
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC,PB:PC=1:2. 
(1)求证:AC平分∠BAD;
(2)探究线段PB,AB之间的数量关系,并说明理由;
(3)若AD=3,求△ABC的面积.
【答案】
(1)证明:连接OC,
∵PE是⊙O的切线,
∴OC⊥PE,
∵AE⊥PE,
∴OC∥AE,
∴∠DAC=∠OCA,
∵OA=OC,
∴∠OCA=∠OAC,
∴∠DAC=∠OAC,
∴AC平分∠BAD
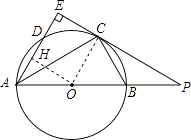
(2)解:线段PB,AB之间的数量关系为:AB=3PB.
理由:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BAC+∠ABC=90°,
∵OB=OC,
∴∠OCB=∠ABC,
∵∠PCB+∠OCB=90°,
∴∠PCB=∠PAC,
∵∠P是公共角,
∴△PCB∽△PAC,
∴ ![]() ,
,
∴PC2=PBPA,
∵PB:PC=1:2,
∴PC=2PB,
∴PA=4PB,
∴AB=3PB
(3)解:过点O作OH⊥AD于点H,则AH= ![]() AD=
AD= ![]() ,四边形OCEH是矩形,
,四边形OCEH是矩形,
∴OC=HE,
∴AE= ![]() +OC,
+OC,
∵OC∥AE,
∴△PCO∽△PEA,
∴ ![]() ,
,
∵AB=3PB,AB=2OB,
∴OB= ![]() PB,
PB,
∴ ![]() =
= ![]() ,
,
∴OC= ![]() ,
,
∴AB=5,
∵△PBC∽△PCA,
∴ ![]() ,
,
∴AC=2BC,
在Rt△ABC中,AC2+BC2=AB2,
∴(2BC)2+BC2=52,
∴BC= ![]() ,
,
∴AC=2 ![]() ,
,
∴S△ABC= ![]() ACBC=5.
ACBC=5.

【解析】(1)首先连接OC,由PE是⊙O的切线,AE和过点C的切线互相垂直,可证得OC∥AE,又由OA=OC,易证得∠DAC=∠OAC,即可得AC平分∠BAD;(2)由AB是⊙O的直径,PE是切线,可证得∠PCB=∠PAC,即可证得△PCB∽△PAC,然后由相似三角形的对应边成比例与PB:PC=1:2,即可求得答案;(3)首先过点O作OH⊥AD于点H,则AH= ![]() AD=
AD= ![]() ,四边形OCEH是矩形,即可得AE=
,四边形OCEH是矩形,即可得AE= ![]() +OC,由OC∥AE,可得△PCO∽△PEA,然后由相似三角形的对应边成比例,求得OC的长,再由△PBC∽△PCA,证得AC=2BC,然后在Rt△ABC中,AC2+BC2=AB2 , 可得(2BC)2+BC2=52 , 即可求得BC的长,继而求得答案.
+OC,由OC∥AE,可得△PCO∽△PEA,然后由相似三角形的对应边成比例,求得OC的长,再由△PBC∽△PCA,证得AC=2BC,然后在Rt△ABC中,AC2+BC2=AB2 , 可得(2BC)2+BC2=52 , 即可求得BC的长,继而求得答案.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】请从以下两个小题中任选一个作答,若多选,则按第一题计分.
A.一个八边形的外角和是°.
B.计划在楼层间修建一个坡角为35°的楼梯,若楼层间高度为2.7m,为了节省成本,现要将楼梯坡角增加11°,则楼梯的斜面长度约减少 m.(用科学计算器计算,结果精确到0.01m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,∠A=30°,BC=1,D为AB中点,E为AC上一动点,BF∥AC交ED延长线于点F,则四边形BCEF周长的最小值为( )

A. 1+![]() B. 4 C. 2+
B. 4 C. 2+![]() D. 2+
D. 2+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,在ABCD中,∠BCD=120°,分别延长DC、BC到点E,F,使得△BCE和△CDF都是正三角形.

(1)求证:AE=AF;
(2)求∠EAF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
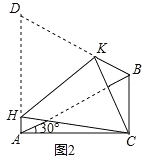
【题目】如图1,在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形,E是AB的中点,连接CE并延长交AD于F.
(1)求证:△AEF≌△BEC;
(2)判断四边形BCFD是何特殊四边形,并说出理由;
(3)如图2,将四边形ACBD折叠,使D与C重合,HK为折痕,若BC=1,求AH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c与⊙M相交于A、B、C、D四点,其中A、B两点的坐标分别为(﹣1,0),(0,﹣2),点D在x轴上且AD为⊙M的直径.点E是⊙M与y轴的另一个交点,过劣弧 ![]() 上的点F作FH⊥AD于点H,且FH=1.5
上的点F作FH⊥AD于点H,且FH=1.5
(1)求点D的坐标及该抛物线的表达式;
(2)若点P是x轴上的一个动点,试求出△PEF的周长最小时点P的坐标;
(3)在抛物线的对称轴上是否存在点Q,使△QCM是等腰三角形?如果存在,请直接写出点Q的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=ax+b和反比例函数y= ![]() 在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( )
在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( ) 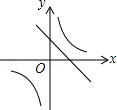
A.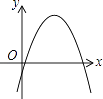
B.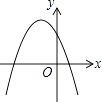
C.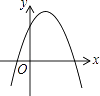
D.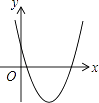
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
国际比赛的足球场长在100m到110m之间,宽在64m到75m之间,为了迎接2015年的亚洲杯,某地建设了一个长方形的足球场,其长是宽的1.5倍,面积是7560m2.请你判断这个足球场能用于国际比赛吗?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com