
【题目】(8分)如图,在ABCD中,∠BCD=120°,分别延长DC、BC到点E,F,使得△BCE和△CDF都是正三角形.

(1)求证:AE=AF;
(2)求∠EAF的度数.
【答案】(1)证明见试题解析;(2)60°.
【解析】
试题(1)根据平行四边形的性质得到∠BAD=∠BCD=120°,∠ABC=∠ADC,AB=CD,BC=AD,根据等边三角形的性质得到BE=BC,DF=CD,∠EBC=∠CDF=60°,即可证出∠ABE=∠FDA,AB=DF,BE=AD,由SAS证明△ABE≌△FDA,得出对应边相等即可;
(2)根据全等三角形的性质得到∠AEB=∠FAD,求出∠AEB+∠BAE=60°,得出∠FAD+∠BAE=60°,即可得出∠EAF的度数.
试题解析:(1)∵四边形ABCD是平行四边形,∴∠BAD=∠BCD=120°,∠ABC=∠ADC,AB=CD,BC=AD,∵△BCE和△CDF都是正三角形,∴BE=BC,DF=CD,∠EBC=∠CDF=60°,∴∠ABE=∠FDA,AB=DF,BE=AD,在△ABE和△FDA中,∵AB=DF,∠ABE=JIAO FDA,BE=AD,∴△ABE≌△FDA(SAS),∴AE=AF;
(2)∵△ABE≌△FDA,∴∠AEB=∠FAD,∵∠ABE=60°+60°=120°,∴∠AEB+∠BAE=60°,∴∠FAD+∠BAE=60°,∴∠EAF=120°﹣60°=60°.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
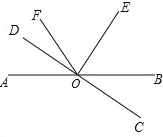
【题目】如图,直线AB与CD相交于点0,∠AOD=20°,∠DOF:∠FOB=1:7,射线OE平分∠BOF.
(1)求∠EOB的度数;
(2)射线OE与直线CD有什么位置关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加某网店的“翻牌抽奖”活动,如图,共有4张牌,分别对应5元,10元,15元,20元的现金优惠券,小明只能看到牌的背面. 
(1)如果随机翻一张牌,那么抽中20元现金优惠券的概率是 .
(2)如果随机翻两张牌,且第一次翻的牌不参与下次翻牌,则所获现金优惠券的总值不低于30元的概率是多少?请画树状图或列表格说明问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣2x3y)2(﹣2xy)+(﹣2x3y)3÷2x2
(2)20202﹣2019×2021
(3)(﹣2a+b+1)(2a+b﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,求证:∠ACD=∠B;
(2)如图②,在Rt△ABC中,∠C=90°,D、E分别在AC,AB上,且∠ADE=∠B,判断△ADE的形状?并说明理由?
(3)如图③,在Rt△ABC和Rt△DBE中,∠C=90°,∠E=90°,点C,B,E在同一直线上,若AB⊥BD,AB=BD,则CE与AC,DE有什么等量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列数量关系列不等式:
(1)a与1的和是正数 ;
(2)a的![]() 和b的
和b的![]() 的差是负数 ;
的差是负数 ;
(3)a与b的两数和的平方不大于9 ;
(4)a的![]() 倍与b的和的平方是非负数 .
倍与b的和的平方是非负数 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC,PB:PC=1:2. 
(1)求证:AC平分∠BAD;
(2)探究线段PB,AB之间的数量关系,并说明理由;
(3)若AD=3,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从家到图书馆看报然后返回,他离家的距离y与离家的时间x之间的对应关系如图所示,如果小明在图书馆看报30分钟,那么他离家50分钟时离家的距离为 km.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.

(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com