
【题目】(1)如图①,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,求证:∠ACD=∠B;
(2)如图②,在Rt△ABC中,∠C=90°,D、E分别在AC,AB上,且∠ADE=∠B,判断△ADE的形状?并说明理由?
(3)如图③,在Rt△ABC和Rt△DBE中,∠C=90°,∠E=90°,点C,B,E在同一直线上,若AB⊥BD,AB=BD,则CE与AC,DE有什么等量关系,并证明.

【答案】(1)证明见解析(2)直角三角形(3)CE=AC+DE
【解析】
(1)根据直角三角形的性质得出∠ACD+∠A=∠B+∠DCB=90°,再解答即可;(2)根据直角三角形的性质得出∠ADE+∠A=∠A+∠B=90°,再解答即可;(3)由AB⊥BD可得∠DBE+∠ABC=90°,进而可证明∠A=∠DBE,利用AAS可证明△ABC≌△BDE,即可证明BC=DE,AC=BE,从而可证明CE=AC+DE.
(1)∵在Rt△ABC中,∠ACB=90°,
∴∠A+∠B =90°,
∵CD⊥AB,
∴∠ACD+∠A=90°,
∴∠ACD=∠B.
(2)△ADE是直角三角形,理由如下:
∵在Rt△ABC中,∠ACB=90°,
∴∠A+∠B =90°,
∵∠ADE=∠B,
∴∠A+∠ADE=90°,
∴∠AED=90°,即△ADE得直角三角形.
(3)CE=AC+DE,证明如下:
∵点C、B、E在同一直线上,AB⊥BD,
∴∠DBE+∠ABC=90°,
∵∠A+∠ABC=90°,
∴∠A=∠DBE
∵∠C=∠E=90°,AB=BD,∠A=∠DBE,
∴△ABC≌△BDE,
∴BC=DE,AC=BE,
∴CE=CB+BE=DE+AC.


科目:初中数学 来源: 题型:
【题目】端午节放假期间,小明和小华准备到宜宾的蜀南竹海(记为A)、兴文石海(记为B)、夕佳山民居(记为C)、李庄古镇(记为D)的一个景点去游玩,他们各自在这四个景点中任选一个,每个景点都被选中的可能性相同.
(1)小明选择去蜀南竹海旅游的概率为 .
(2)用树状图或列表的方法求小明和小华都选择去兴文石海旅游的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,∠A=30°,BC=1,D为AB中点,E为AC上一动点,BF∥AC交ED延长线于点F,则四边形BCEF周长的最小值为( )

A. 1+![]() B. 4 C. 2+
B. 4 C. 2+![]() D. 2+
D. 2+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次篮球联赛初赛阶段,每队有![]() 场比赛,每场比赛都要分出胜负,每队胜一场得
场比赛,每场比赛都要分出胜负,每队胜一场得![]() 分, 负一场得
分, 负一场得![]() 分,积分超过
分,积分超过![]() 分才能获得参赛资格.
分才能获得参赛资格.
(1)已知甲队在初赛阶段的积分为![]() 分,求甲队初赛阶段胜、负各多少场;
分,求甲队初赛阶段胜、负各多少场;
(2)如果乙队要获得参加决赛资格,那么乙队在初赛阶段至少要胜多少场?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,在ABCD中,∠BCD=120°,分别延长DC、BC到点E,F,使得△BCE和△CDF都是正三角形.

(1)求证:AE=AF;
(2)求∠EAF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形,E是AB的中点,连接CE并延长交AD于F.
(1)求证:△AEF≌△BEC;
(2)判断四边形BCFD是何特殊四边形,并说出理由;
(3)如图2,将四边形ACBD折叠,使D与C重合,HK为折痕,若BC=1,求AH的长.

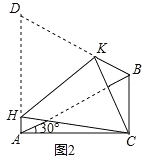
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=ax+b和反比例函数y= ![]() 在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( )
在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( ) 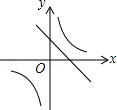
A.
B.
C.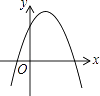
D.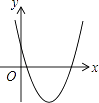
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据不等式的基本性质,把下列不等式化成“x>a”或“x<a”的形式:
(1)4x>3x+5 (2)-2x<17
(3)0.3x<-0.9 (4)x<![]() x-4
x-4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com