
【题目】如图,Rt△ABC中,∠C=90°,∠A=30°,BC=1,D为AB中点,E为AC上一动点,BF∥AC交ED延长线于点F,则四边形BCEF周长的最小值为( )

A. 1+![]() B. 4 C. 2+
B. 4 C. 2+![]() D. 2+
D. 2+![]()
【答案】C
【解析】
由△ADE≌△BDF,推出BF=AE,推出四边形BCEF的周长=BC+CE+EF+BF=BC+AC+EF,由题意易知BC=1,AC=![]() ,即可推出EF最小时,四边形BCEF的周长最小,当DE⊥AC时,EF的值最小.
,即可推出EF最小时,四边形BCEF的周长最小,当DE⊥AC时,EF的值最小.
∵BF∥AC,
∴∠A=∠FBD,
在△ADE和△BDF中,
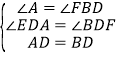 ,
,
∴△ADE≌△BDF,
∴BF=AE,
∴四边形BCEF的周长=BC+CE+EF+BF=BC+AC+EF,
由题意易知BC=1,AC=![]() ,
,
∴EF最小时,四边形BCEF的周长最小,当DE⊥AC时,EF的值最小,
∵BD=AD,DE∥CB,
∴CE=AE,
∴DE=![]() BC=
BC=![]() ,
,
∴EF=2DE=1,
∴四边形BCEF周长的最小值为2+![]() .
.
故答案选C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】先化简,再求值:
(1)(x+y)(x-y)-x(x+y)+2xy,其中x=(3-π)0,y=(![]() )-1;
)-1;
(2)(2a+b)2-(2a-b)(a+b)-2(a-2b)(a+2b),其中a=![]() ,b=-2.
,b=-2.
查看答案和解析>>
科目:初中数学 来源: 题型:
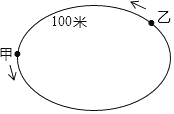
【题目】已知甲沿周长为300米的环形跑道按逆时针方向跑步,速度为a米/秒,与此同时在甲后面100米的乙也沿该环形跑道按逆时针方向跑步,速度为3米/秒.
(1)若a=1,求甲、乙两人第一次相遇所用的时间;
(2)若a>3,甲、乙两人第一次相遇所用的时间为80秒,试求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加某网店的“翻牌抽奖”活动,如图,共有4张牌,分别对应5元,10元,15元,20元的现金优惠券,小明只能看到牌的背面. 
(1)如果随机翻一张牌,那么抽中20元现金优惠券的概率是 .
(2)如果随机翻两张牌,且第一次翻的牌不参与下次翻牌,则所获现金优惠券的总值不低于30元的概率是多少?请画树状图或列表格说明问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A(1,2),解答以下问题:
(1)请在图中建立适当的直角坐标系,并写出图书馆B位置的坐标;

(2)若体育馆位置坐标为C(-3,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣2x3y)2(﹣2xy)+(﹣2x3y)3÷2x2
(2)20202﹣2019×2021
(3)(﹣2a+b+1)(2a+b﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,求证:∠ACD=∠B;
(2)如图②,在Rt△ABC中,∠C=90°,D、E分别在AC,AB上,且∠ADE=∠B,判断△ADE的形状?并说明理由?
(3)如图③,在Rt△ABC和Rt△DBE中,∠C=90°,∠E=90°,点C,B,E在同一直线上,若AB⊥BD,AB=BD,则CE与AC,DE有什么等量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC,PB:PC=1:2. 
(1)求证:AC平分∠BAD;
(2)探究线段PB,AB之间的数量关系,并说明理由;
(3)若AD=3,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com