
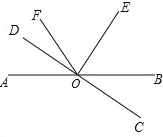
【题目】如图,直线AB与CD相交于点0,∠AOD=20°,∠DOF:∠FOB=1:7,射线OE平分∠BOF.
(1)求∠EOB的度数;
(2)射线OE与直线CD有什么位置关系?请说明理由.
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】在正整数中,
(1﹣![]() )=(1﹣
)=(1﹣![]() )(1+
)(1+![]() )
)
(1﹣![]() )=(1﹣
)=(1﹣![]() )(1+
)(1+![]() )
)
(1﹣![]() )=(1﹣
)=(1﹣![]() )(1+
)(1+![]() )
)
观察上面的算式,可以归纳得出:![]() = .
= .
利用上述规律,计算下列各式:(1﹣![]() )×(1﹣
)×(1﹣![]() )×(1﹣
)×(1﹣![]() )= .
)= .
(1﹣![]() )×(1﹣
)×(1﹣![]() )×(1﹣
)×(1﹣![]() )×…×(1﹣
)×…×(1﹣![]() )= (请将结题步骤写在下方空白处)
)= (请将结题步骤写在下方空白处)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节放假期间,小明和小华准备到宜宾的蜀南竹海(记为A)、兴文石海(记为B)、夕佳山民居(记为C)、李庄古镇(记为D)的一个景点去游玩,他们各自在这四个景点中任选一个,每个景点都被选中的可能性相同.
(1)小明选择去蜀南竹海旅游的概率为 .
(2)用树状图或列表的方法求小明和小华都选择去兴文石海旅游的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区将原来400平方米的正方形场地改建成300平方米的长方形场地,且长和宽之比为3∶2.如果把原来正方形场地的铁栅栏围墙利用起来围成新场地的长方形围墙,那么这些铁栅栏是否够用?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请从以下两个小题中任选一个作答,若多选,则按第一题计分.
A.一个八边形的外角和是°.
B.计划在楼层间修建一个坡角为35°的楼梯,若楼层间高度为2.7m,为了节省成本,现要将楼梯坡角增加11°,则楼梯的斜面长度约减少 m.(用科学计算器计算,结果精确到0.01m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点A、D在y轴正半轴上,点B、C分别在x轴上,CD平分∠ACB,与y轴交于D点,∠CAO=90°-∠BDO.
(1)求证:AC=BC:
(2)如图2,点C的坐标为(4,0),点E为AC上一点,且∠DEA=∠DBO,求BC+EC的长;

(3)如图3,过D作DF⊥AC于F点,点H为FC上一动点,点G为OC上一动点,当H在FC上移动、点G在OC上移动时,始终满足∠GDH=∠GDO+∠FDH,试判断FH、GH、OG这三者之间的数量关系,写出你的结论并加以证明.
 (图3)
(图3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,在ABCD中,∠BCD=120°,分别延长DC、BC到点E,F,使得△BCE和△CDF都是正三角形.

(1)求证:AE=AF;
(2)求∠EAF的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com