
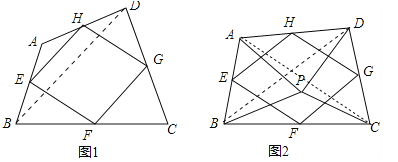
����Ŀ�����Ǹ������¶��壺˳����������һ���ı��θ����е����õ��ı��ν��е��ı��Σ�

��1����ͼ1���ı���ABCD�У���E��F��G��H�ֱ�Ϊ��AB��BC��CD��DA���е㣮��֤���е��ı���EFGH��ƽ���ı��Σ�
��2����ͼ2����P���ı���ABCD��һ�㣬������PA=PB��PC=PD����APB=��CPD����E��F��G��H�ֱ�Ϊ��AB��BC��CD��DA���е㣬�����е��ı���EFGH����״����֤����IJ��룻
��3�����ı䣨2���е�������ʹ��APB=��CPD=90�㣬�����������䣬ֱ��д���е��ı���EFGH����״��������֤����
���𰸡���1��֤������������2���ı���EFGH����������3���ı���EFGH�������Σ�
��������
�����������1����ͼ1�У�����BD��������������λ�߶���ֻҪ֤��EH��FG��EH=FG���ɣ�
��2���ı���EFGH�����Σ���֤����APC�ա�BPD���õ�AC=BD����֤��EF=FG���ɣ�
��3���ı���EFGH�������Σ�ֻҪ֤����EHG=90�㣬���á�APC�ա�BPD���á�ACP=��BDP������֤����COD=��CPD=90�㣬�ٸ���ƽ���ߵ����ʼ���֤����
�����������1��֤������ͼ1�У�����BD��
�ߵ�E��H�ֱ�Ϊ��AB��DA���е㣬��EH��BD��EH=![]() BD���ߵ�F��G�ֱ�Ϊ��BC��CD���е㣬��FG��BD��FG=
BD���ߵ�F��G�ֱ�Ϊ��BC��CD���е㣬��FG��BD��FG=![]() BD����EH��FG��EH=GF�����е��ı���EFGH��ƽ���ı��Σ�
BD����EH��FG��EH=GF�����е��ı���EFGH��ƽ���ı��Σ�
��2���ı���EFGH�����Σ�
֤������ͼ2�У�����AC��BD��
�ߡ�APB=��CPD�����APB+��APD=��CPD+��APD������APC=��BPD���ڡ�APC�͡�BPD�У���AP=PB����APC=��BPD��PC=PD�����APC�ա�BPD����AC=BD���ߵ�E��F��G�ֱ�Ϊ��AB��BC��CD���е㣬��EF=![]() AC��FG=
AC��FG=![]() BD�����ı���EFGH��ƽ���ı��Σ����ı���EFGH�����Σ�
BD�����ı���EFGH��ƽ���ı��Σ����ı���EFGH�����Σ�
��3���ı���EFGH�������Σ�
֤������ͼ2�У���AC��BD���ڵ�O��AC��PD���ڵ�M��AC��EH���ڵ�N��
�ߡ�APC�ա�BPD�����ACP=��BDP���ߡ�DMO=��CMP�����COD=��CPD=90�㣬��EH��BD��AC��HG�����EHG=��ENO=��BOC=��DOC=90�㣬���ı���EFGH�����Σ����ı���EFGH�������Σ�


 ���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����A��B����Ʒ�ƵĽ�ѧ�豸�������ֽ�ѧ�豸�Ľ��ۺ��ۼ����±���ʾ��
A | B | |
���ۣ���Ԫ/�ף� | 1.5 | 1.2 |
�ۼۣ���Ԫ/�ף� | 1.65 | 1.4 |
���̳��ƻ��������ֽ�ѧ�豸�����ף�����66��Ԫ��ȫ�����ۺ�ɻ�ë����9��Ԫ��
��ë����=���ۼ� - ���ۣ�����������
��1�����̳��ƻ�����A��B����Ʒ�ƵĽ�ѧ�豸�������ף�
��2��ͨ���г����У����̳�������ԭ�ƻ��Ļ����ϣ�����A���豸�Ĺ�������������B���豸�Ĺ�����������֪B���豸���ӵ�������A����������������1.5���������ڹ��������ֽ�ѧ�豸�����ʽ���69��Ԫ����A���豸��������������ٶ����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
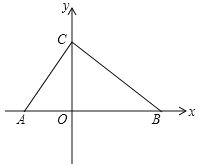
����Ŀ����ͼ����ƽ��ֱ������ϵ�ڣ��� O Ϊ����ԭ�㣬�� A �� x �Ḻ�����ϣ��� B��C �ֱ��� x �ᡢy ���������ϣ��� OB=2OA��OB��OC=OC��OA=2��
��1����� C �����ꣻ
��2���� P �ӵ� A ������ÿ�� 1 ����λ���ٶ��� AB ��� B �����˶���ͬʱ�� Q �ӵ� B ���� ��ÿ�� 3 ����λ���ٶ��� BA ���յ� A �����˶������� Q �����յ� A ʱ���� P��Q ��ֹͣ�� ������� P �˶���ʱ��Ϊ t �루t��0�����߶� PQ �ij���Ϊ y���ú� t ��ʽ�ӱ�ʾ y����д�� ��Ӧ�� t �ķ�Χ��
��3���ڣ�2���������£����� P �� x ��Ĵ��� PM��PM=PQ���Ƿ���� t ֵʹ�� O Ϊ PQ �� �㣿�������� t ֵ�������ʱ������ CMQ ��������������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽ��ÿ��С�����εı߳���Ϊ1���ı���ABCD���ĸ����㶼��С�����εĶ��㣨С�����εĶ���и�㣩�ϣ�����BD��

��1�����ø����ͼ�л�����ABD��AD���ϵĸߣ�����ΪH��
��2���ٻ�������ABD������ƽ��2��������ƽ��2��õ�����A1B1D1��
��ƽ�ƺ����߶�ABɨ���IJ�������ɵķ��ͼ�ε������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ƽ���ı���ABCD�У�CEƽ�֡�BCD�ҽ�AD�ڵ�E��A F��CE���ҽ�BC�ڵ�F��
��1����֤����ABF�ա�CDE��
��2����ͼ������1=65�㣬���B�Ĵ�С��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��E��ABCD�ı�CD���е㣬�ӳ�AE��BC���ӳ����ڵ�F��
��1����֤����ADE�ա�FCE��
��2������BAF=90�㣬BC=5��EF=3����CD�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
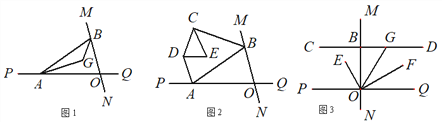
����Ŀ��ֱ��MN��ֱ��PQ�ཻ��O����A������OP�ϣ���B������OM�ϣ�
��1����ͼ1��![]() ��֪AG��BG�ֱ��ǡ�BAO�͡�ABO�ǵ�ƽ���ߣ���
��֪AG��BG�ֱ��ǡ�BAO�͡�ABO�ǵ�ƽ���ߣ���![]() �Ķ�����
�Ķ�����
��2����ͼ2��![]() ��֪AB��ƽ��CD��AD��BC�ֱ��ǡ�BAP�͡�ABM�Ľ�ƽ���ߣ���DE��CE�ֱ��ǡ�ADC�͡�BCD�Ľ�ƽ���ߣ���CED= �ȣ�
��֪AB��ƽ��CD��AD��BC�ֱ��ǡ�BAP�͡�ABM�Ľ�ƽ���ߣ���DE��CE�ֱ��ǡ�ADC�͡�BCD�Ľ�ƽ���ߣ���CED= �ȣ�
��3����ͼ3��![]() ������B��ֱ��CD��MN��GΪ����BD��һ�㣬OFƽ�֡�QOG��OE��OF��̽��
������B��ֱ��CD��MN��GΪ����BD��һ�㣬OFƽ�֡�QOG��OE��OF��̽��![]() �Ĵ�С�Ƿ����仯�������䣬����ֵ�����ı䣬˵�����ɣ�
�Ĵ�С�Ƿ����仯�������䣬����ֵ�����ı䣬˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��DE��BF����1���2����.
��1����˵����FG��AB;
��2������CFG=60������2=150�㣬��DE��AC��ֱ����˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A��3��3����B��5��3����
��1����y��ĸ���������һ��C����ͼ����ʹ���ı���AOCB�����Ϊ18����C������ꣻ
��2������ABO������ƽ��2����λ��������ƽ��4����λ������A1B1O1
��ֱ��д��B1�����꣺B1���� ����
����ƽ�ƹ������߶�OBɨ���������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com