
【题目】如图,在平面直角坐标系内,点 O 为坐标原点,点 A 在 x 轴负半轴上,点 B、C 分别在 x 轴、y 轴正半轴上,且 OB=2OA,OB﹣OC=OC﹣OA=2.
(1)求点 C 的坐标;
(2)点 P 从点 A 出发以每秒 1 个单位的速度沿 AB 向点 B 匀速运动,同时点 Q 从点 B 出发 以每秒 3 个单位的速度沿 BA 向终点 A 匀速运动,当点 Q 到达终点 A 时,点 P、Q 均停止运 动,设点 P 运动的时间为 t 秒(t>0),线段 PQ 的长度为 y,用含 t 的式子表示 y,并写出 相应的 t 的范围;
(3)在(2)的条件下,过点 P 作 x 轴的垂线 PM,PM=PQ,是否存在 t 值使点 O 为 PQ 中 点?若存在求 t 值并求出此时三角形 CMQ 的面积;若不存在,请说明理由.
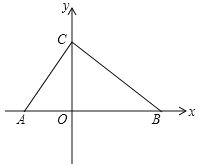
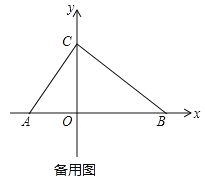
【答案】(1)点 C 的坐标为(0,6);(2)y=12﹣4t(0<t≤3),y=4t﹣12(3<t≤4);(3)存在 t 值使点 O 为 PQ 中点,三角形 CMQ 的面积为:8 或 16.
【解析】分析:(1)设A(x,0),则OA=-x,OB=-2x,OC=-2x-2,进而可得B(-2x,0),C(0,-2x-2),然后根据OC-OA=2,可得x=-4,进而可得点C的坐标;
(2)由(1)可知AB=OA+OB=12,由点Q从点B出发以每秒3个单位的速度沿BA向终点A匀速运动,当点Q到达终点A时,点P、Q均停止运动,可得t的最大值为4秒,然后求出P、Q两点相遇时的t的值为:12÷(1+3)=3秒,然后分两种情况讨论即可:①0<t≤3;②3<t≤4;
(3)点O为PQ中点,可知0<t≤3,OP=OQ,即OA-AP=OB-BP,进而可求t的值;然后分两种情况讨论即可:①点M在x轴上方;②点M在x轴下方.
详解:(1)∵点A在x轴负半轴上,点B、C分别在x轴、y轴正半轴上,OB=2OA,
OB﹣OC=OC﹣OA=2.设A(x,0),
∴OA=﹣x,OB=﹣2x,OC=﹣2x﹣2,
∴B(﹣2x,0),C(0,﹣2x﹣2),
∵OC﹣OA=2,
∴﹣2x﹣2﹣(﹣x)=2,解得:x=﹣4,
∴OA=4,OB=8,OC=6,点A的坐标为(﹣4,0),点B的坐标为(8,0),点C的坐标为(0,6);
(2)由(1)知:AB=OA+OB=12,
∵点P从点A出发以每秒1个单位的速度沿AB向点B匀速运动,同时点Q从点B出发以每秒3个单位的速度沿BA向终点A匀速运动,
∴点P运动的时间为t(t>0)秒时,AP=t,BQ=3t,当P、Q两点相遇时的t的值为:12÷(1+3)=3秒,
∵当点Q到达终点A时,点P、Q均停止运动,
∴t的最大值为12÷3=4秒.
①当0<t≤3时,如图1,
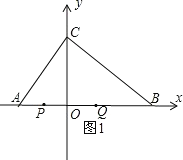
PQ=AB﹣AP﹣QB=12﹣t﹣3t=12﹣4t,
即y=12﹣4t(0<t≤3);
②当3<t≤4时,如图2,
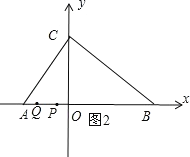
PQ=AP+BQ-AB=4t-12,即y=4t-12(![]() ).
).
(3)存在t值使点O为PQ中点,
∵点O为PQ中点,
∴0<t≤3,OP=OQ,即OA﹣AP=OB﹣BQ,
∴4-t=8-3t,
当t=2时,AP=2,OP=2,OQ=2,PQ=4,PM=PQ=4,
①点M在x轴上方时,如图3,
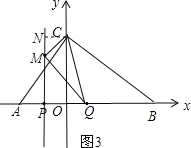
过点C作CN⊥PM,得:四边形CNPQ是梯形,
∵S△CMQ=S梯形CNPQ﹣S△CNM﹣S△PQM,
∴S△CMQ=![]() (CN+PQ)×PN﹣
(CN+PQ)×PN﹣![]() CNMN﹣
CNMN﹣![]() PMPQ,
PMPQ,
=![]() (OP+PQ)×OC﹣
(OP+PQ)×OC﹣![]() ×OP×(OC﹣PM)﹣
×OP×(OC﹣PM)﹣![]() ×4×4,
×4×4,
=![]() (2+4)×6﹣
(2+4)×6﹣![]() 2×(6﹣4)﹣8,
2×(6﹣4)﹣8,
=18﹣2﹣8,
=8;
②点M在x轴下方,如图4.
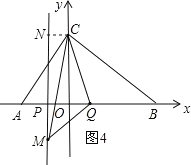
过点C作CN⊥PM,得:四边形CNPQ是梯形,
∵S△CMQ=S梯形CNPQ+S△PQM﹣S△CNM,
∴S△CMQ=![]() (CN+PQ)PN+
(CN+PQ)PN+![]() PQPM﹣
PQPM﹣![]() MNCN,
MNCN,
=![]() (OP+PQ)×OC+
(OP+PQ)×OC+![]() ×4×4﹣
×4×4﹣![]() (OC+PM)OP,
(OC+PM)OP,
=![]() (2+4)×6+8﹣
(2+4)×6+8﹣![]() (6+4)×2,
(6+4)×2,
=![]() +8﹣
+8﹣![]() ,
,
=18+8﹣10,
=16.
∴三角形CMQ的面积为:8或16.


科目:初中数学 来源: 题型:
【题目】小高从家骑自行车去学校上学,先走上坡路到达点A,再走下坡路到达点B,最后走平路到达学校,所用的时间与路程的关系如图所示.放学后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上学时一致,那么他从学校到家需要的时间是( ) 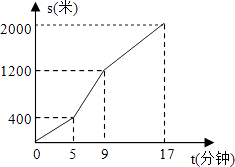
A.14分钟
B.17分钟
C.18分钟
D.20分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ACB中,∠C=90°,BE平分∠ABC,ED垂直平分AB于D,则图中的全等三角形对数共有( )
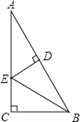
A. 1对 B. 2对 C. 3对 D. 4对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛掷一个质地均匀且六个面上依次刻有1﹣6的点数的正方体型骰子,如图.观察向上的一面的点数,下列情况属必然事件的是( ) 
A.出现的点数是7
B.出现的点数不会是0
C.出现的点数是2
D.出现的点数为奇数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们把横、纵坐标都是整数的点叫做整点,且规定:正方形内部 不包含边界上的点.观察如图所示的中心在原点、一边平行于 x 轴的正方形:边长为 1 的正方形内部有 1 个整点,边长为 2 的正方形内部有 1 个整点,边长为 3 的正方形内部 有 9 个整点,…,则边长为 10 的正方形内的整点个数为( )

A. 64 个 B. 100 个 C. 81 个 D. 121 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组研究我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.
(1)求该店有客房多少间?房客多少人?
(2)假设店主李三公将客房进行改造后,房间数大大增加.每间客房收费20钱,且每间客房最多入住4人,一次性定客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何订房更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.

(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=![]() BC,连接CD和EF.
BC,连接CD和EF.
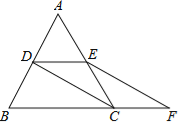
(1)求证:DE=CF;
(2)求EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com