练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】小高从家骑自行车去学校上学，先走上坡路到达点A，再走下坡路到达点B，最后走平路到达学校，所用的时间与路程的关系如图所示．放学后，如果他沿原路返回，且走平路、上坡路、下坡路的速度分别保持和去上学时一致，那么他从学校到家需要的时间是（ ）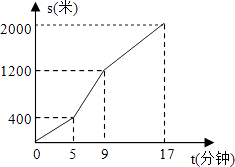
    A.14分钟
    B.17分钟
    C.18分钟
    D.20分钟

    【答案】D
    【解析】解：上坡的速度是：400÷5=80米/分钟； 下坡的速度是：（1200﹣400）÷（9﹣5）=200米/分钟；
    平路的速度是：（2000﹣1200）÷（17﹣9）=100米/分钟．
    则从学校到家需要的时间是： + + =20分钟．
    故选：D．
    【考点精析】认真审题，首先需要了解函数的图象(函数的图像是由直角坐标系中的一系列点组成；图像上每一点坐标（x，y）代表了函数的一对对应值，他的横坐标x表示自变量的某个值，纵坐标y表示与它对应的函数值)．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知：如图，点C在AOB的一边OA上，过点C的直线DE//OB，CF平分ACD，CG CF于C ．

    （1）若O =40，求ECF的度数；

    （2）求证：CG平分OCD；

    （3）当O为多少度时，CD平分OCF，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市有三个景区是人们节假日游玩的热点景区，某学校对七（1）班学生“五一”小长假随父母到这三个景区游玩的计划做了全面调查，调查分四个类别，A：三个景区；B：游两个景区；C：游一个景区；D：不到这三个景区游玩，现根据调查结果绘制了如下不完全的条形统计图和扇形统计图，请结合图中信息解答下列问题：

    （1）九（1）班现有学生__________人，在扇形统计图中表示“B类别”的扇形的圆心角的度数为__________；

    （2）请将条形统计图补充完整；

    （3）若该校七年级有1000名学生，求计划“五一”小长假随父母到这三个景区游玩的学生多少名？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法正确的是（ ）

    A.互为相反数的两数绝对值一定相等B.互为相反数的两数相乘，积一定是负数

    C.绝对值等于它本身的数是正数D.零的相反数没有意义

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线的顶点是C（0，a）（a＞0，a为常数），并经过点（2a，2a），点D（0，2a）为一定点．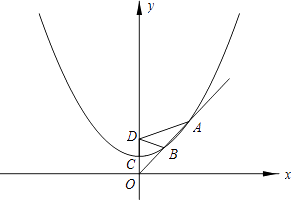

    （1）求含有常数a的抛物线的解析式；
    （2）设点P是抛物线上任意一点，过P作PH丄x轴．垂足是H，求证：PD=PH；
    （3）设过原点O的直线l与抛物线在笫一象限相交于A、B两点，若DA=2DB．且S△ABD=4 ．求a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某公交公司有A，B型两种客车，它们的载客量和租金如下表：

    A

    B

    载客量（人/辆）

    45

    30

    租金（元/辆）

    400

    280

    某中学根据实际情况，计划租用A，B型客车共5辆，同时送七年级师生到基地校参加社会实践活动．设租用A型客车x辆，根据要求回答下列问题：

    （1）用含x的式子填写下表：

    车辆数（辆）

    载客量

    租金（元）

    A

    x

    45x

    400x

    B

    5﹣x

    　 　

    　 　

    （2）若要保证租车费用不超过1900元，求x的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了解某市市民“绿色出行”方式的情况，某校数学兴趣小组以问卷调查的形式，随机调查了某市部分出行市民的主要出行方式（参与问卷调查的市民都只从以下五个种类中选择一类），并将调查结果绘制成如下不完整的统计图．

    种类

    A

    B

    C

    D

    E

    出行方式

    共享单车

    步行

    公交车

    的士

    私家车

    根据以上信息，回答下列问题：

    （1）参与本次问卷调查的市民共有 人，其中选择B类的人数有 人；

    （2）在扇形统计图中，求A类对应扇形圆心角α的度数，并补全条形统计图；

    （3）该市约有12万人出行，若将A，B，C这三类出行方式均视为“绿色出行”方式，请估计该市“绿色出行”方式的人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商场销售A，B两种品牌的教学设备，这两种教学设备的进价和售价如下表所示：

    A

    B

    进价（万元/套）

    1.5

    1.2

    售价（万元/套）

    1.65

    1.4

    该商场计划购进两种教学设备若干套，共需66万元，全部销售后可获毛利润9万元。

    （毛利润=（售价 - 进价）×销售量）

    （1）该商场计划购进A，B两种品牌的教学设备各多少套？

    （2）通过市场调研，该商场决定在原计划的基础上，减少A种设备的购进数量，增加B种设备的购进数量，已知B种设备增加的数量是A种设备减少数量的1.5倍。若用于购进这两种教学设备的总资金不超过69万元，问A种设备购进数量至多减少多少套？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系内，点 O 为坐标原点，点 A 在 x 轴负半轴上，点 B、C 分别在 x 轴、y 轴正半轴上，且 OB=2OA，OB﹣OC=OC﹣OA=2．

    （1）求点 C 的坐标；

    （2）点 P 从点 A 出发以每秒 1 个单位的速度沿 AB 向点 B 匀速运动，同时点 Q 从点 B 出发 以每秒 3 个单位的速度沿 BA 向终点 A 匀速运动，当点 Q 到达终点 A 时，点 P、Q 均停止运 动，设点 P 运动的时间为 t 秒（t＞0），线段 PQ 的长度为 y，用含 t 的式子表示 y，并写出 相应的 t 的范围；

    （3）在（2）的条件下，过点 P 作 x 轴的垂线 PM，PM=PQ，是否存在 t 值使点 O 为 PQ 中 点？若存在求 t 值并求出此时三角形 CMQ 的面积；若不存在，请说明理由．

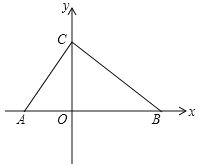
    查看答案和解析>>

    同步练习册答案