
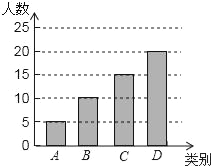
【题目】某市有三个景区是人们节假日游玩的热点景区,某学校对七(1)班学生“五一”小长假随父母到这三个景区游玩的计划做了全面调查,调查分四个类别,A:三个景区;B:游两个景区;C:游一个景区;D:不到这三个景区游玩,现根据调查结果绘制了如下不完全的条形统计图和扇形统计图,请结合图中信息解答下列问题:
(1)九(1)班现有学生__________人,在扇形统计图中表示“B类别”的扇形的圆心角的度数为__________;
(2)请将条形统计图补充完整;
(3)若该校七年级有1000名学生,求计划“五一”小长假随父母到这三个景区游玩的学生多少名?

【答案】(1)50;72°;(2)补图见解析;(3)计划“五一”小长假随父母到这三个景区游玩的学生人数是600人.
【解析】试题分析:(1)根据图象得到信息.(2)先算出总人数,再分别计算度数,补充统计图.
(3)用总人数乘以去三个景区的百分比.
试题解析:
解:(1)∵A类5人,占10%,
∴八(1)班共有学生有:5÷10%=50(人);
∴在扇形统计图中,表示“B类别”的扇形的圆心角的度数为: ![]() ×360°=72°;
×360°=72°;
故答案为:50,72°.
(2)D类:50﹣5﹣10﹣15=20(人),如图:
 ;
;
(3)计划“五一”小长假随父母到这三个景区游玩的学生人数是1000×(1﹣![]() )=600(人).
)=600(人).
答:计划“五一”小长假随父母到这三个景区游玩的学生人数是600人.


 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线AB与x轴、y轴分别交于点A,B,与反比例函数 ![]() (k为常数,且k>0)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若
(k为常数,且k>0)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若 ![]() (m为大于l的常数).记△CEF的面积为S1 , △OEF的面积为S2 , 则
(m为大于l的常数).记△CEF的面积为S1 , △OEF的面积为S2 , 则 ![]() = . (用含m的代数式表示)
= . (用含m的代数式表示)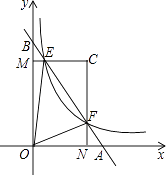
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好地治理小凌河水质,保护环境,市治污公司决定购买10台污水处理设备,现有A 、B两种设备,A 、B单价分别为a万元/台、 b万元/台,月处理污水分别为240吨/月、200吨/月,经调查,买一台A型设备比买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
(1)求a、b的值.
(2)经预算,市治污公司购买污水处理器的资金不超过105万元,你认为该公司有哪几种购买方案?
(3)在(2)的条件下,若每月处理的污水不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:
以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;再以A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2;再以A2为圆心,1为半径向右画弧交OC于点A3,得第3条线段A2A3;…这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n=______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线![]() ,直线
,直线![]() 与
与![]() 、
、![]() 分别交于C、D两点,点P是直线
分别交于C、D两点,点P是直线![]() 上的一动点.
上的一动点.
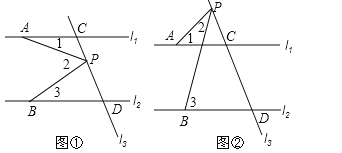
(1)如图,若动点P在线段CD之间运动(不与C、D两点重合),问在点P的运动过程中是否始终具有![]() 这一相等关系?试说明理由;
这一相等关系?试说明理由;
(2)如图,当动点P在线段CD之外且在![]() 的上方运动(不与C、D两点重合),则上述结论是否仍成立?若不成立,试写出新的结论,并说明理由;
的上方运动(不与C、D两点重合),则上述结论是否仍成立?若不成立,试写出新的结论,并说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小高从家骑自行车去学校上学,先走上坡路到达点A,再走下坡路到达点B,最后走平路到达学校,所用的时间与路程的关系如图所示.放学后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上学时一致,那么他从学校到家需要的时间是( ) 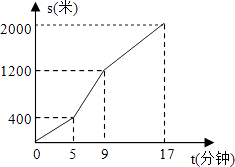
A.14分钟
B.17分钟
C.18分钟
D.20分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ACB中,∠C=90°,BE平分∠ABC,ED垂直平分AB于D,则图中的全等三角形对数共有( )
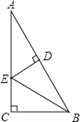
A. 1对 B. 2对 C. 3对 D. 4对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com